Remap 3D Cubic Spline Interpolation code by Python
10 Oct 2024 14:08 - 10 Oct 2024 14:30 #311727
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
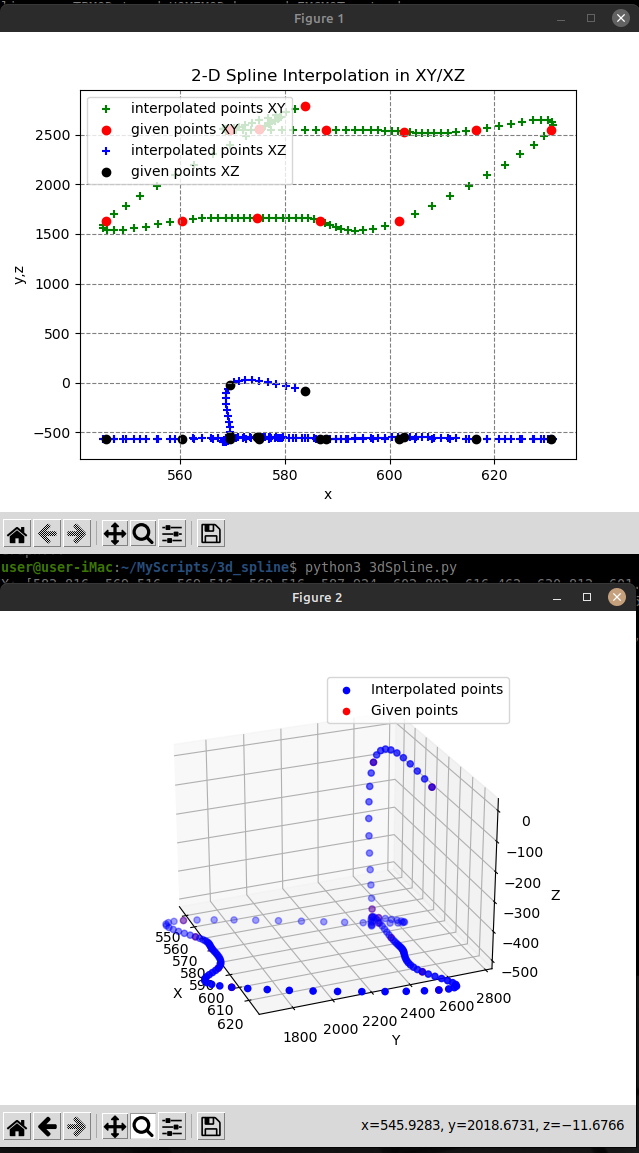
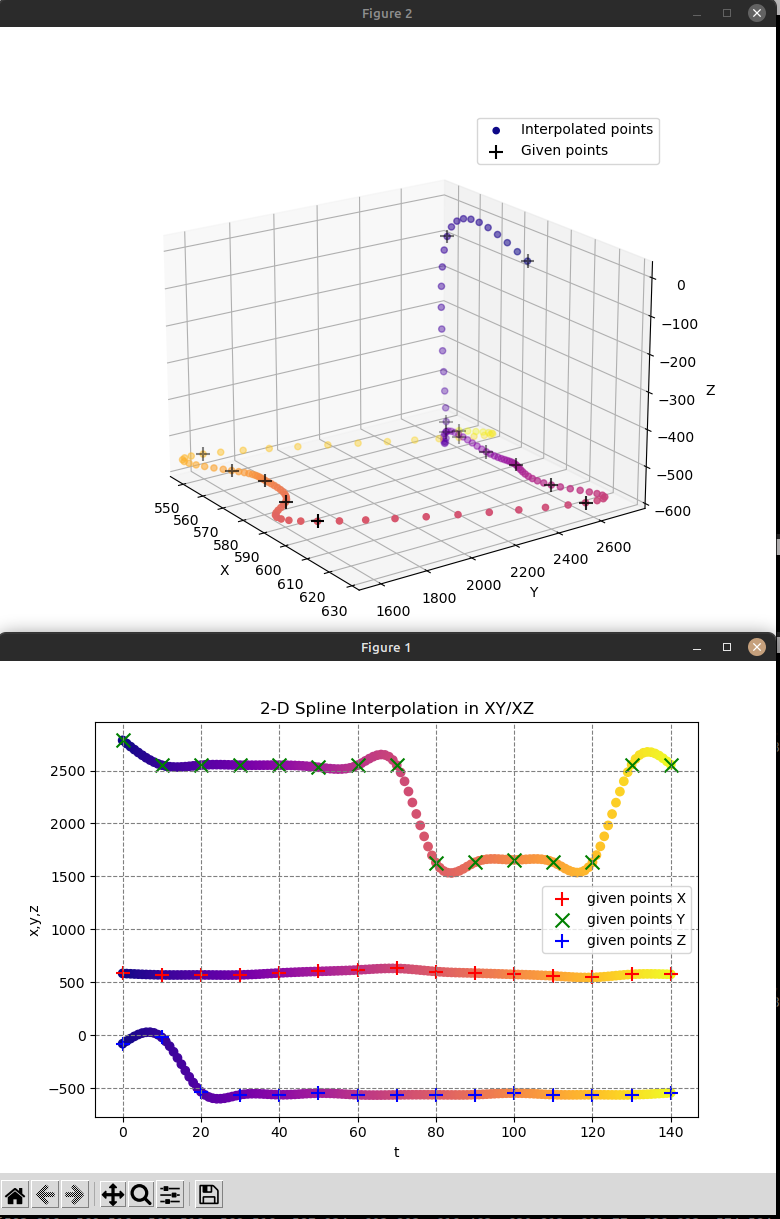
Modified the script to accept any sequence of point coordinates (x,y,z) read from a file called 'points_input.txt' in the same directory as the '3dSpline.py' script and outputs the interpolated points to a file called 'output_file.txt':
The 'points_input.txt' for the example below:
which gives me this output:
[/code]
And the 'output_file.txt' content created:
#! /usr/local/bin/python3.6
"""
3-D spline interpolation
(with graph drawing by matplotlib)
"""
import matplotlib.pyplot as plt
import sys
import os
import traceback
class SplineInterpolation:
def __init__(self, ts, ds):
""" Initialization
:param list ts: item number list of given points
:param list ds: coordinate list of given points
"""
self.ts, self.ds = ts, ds
self.n = len(self.ts) - 1
h = self.__calc_h()
w = self.__calc_w(h)
matrix = self.__gen_matrix(h, w)
v = [0] + self.__gauss_jordan(matrix) + [0]
self.b = self.__calc_b(v)
self.a = self.__calc_a(v)
self.d = self.__calc_d()
self.c = self.__calc_c(v)
def interpolate(self, t):
""" Interpolation
:param float t: value for a interpolate target
:return float : computated y-value
"""
try:
i = self.__search_i(t)
return self.a[i] * (t - self.ts[i]) ** 3 \
+ self.b[i] * (t - self.ts[i]) ** 2 \
+ self.c[i] * (t - self.ts[i]) \
+ self.d[i]
except Exception as e:
raise
def __calc_h(self):
""" H calculation
:return list: h-values
"""
try:
return [self.ts[i + 1] - self.ts[i] for i in range(self.n)]
except Exception as e:
raise
def __calc_w(self, h):
""" W calculation
:param list h: h-values
:return list : w-values
"""
try:
return [
6 * ((self.ds[i + 1] - self.ds[i]) / h[i]
- (self.ds[i] - self.ds[i - 1]) / h[i - 1])
for i in range(1, self.n)
]
except Exception as e:
raise
def __gen_matrix(self, h, w):
""" Matrix generation
:param list h: h-values
:param list w: w-values
:return list mtx: generated 2-D matrix
"""
mtx = [[0 for _ in range(self.n)] for _ in range(self.n - 1)]
try:
for i in range(self.n - 1):
mtx[i][i] = 2 * (h[i] + h[i + 1])
mtx[i][-1] = w[i]
if i == 0:
continue
mtx[i - 1][i] = h[i]
mtx[i][i - 1] = h[i]
return mtx
except Exception as e:
raise
def __gauss_jordan(self, matrix):
""" Solving of simultaneous linear equations
with Gauss-Jordan's method
:param list mtx: list of 2-D matrix
:return list v: answers list of simultaneous linear equations
"""
v = []
n = self.n - 1
try:
for k in range(n):
p = matrix[k][k]
for j in range(k, n + 1):
matrix[k][j] /= p
for i in range(n):
if i == k:
continue
d = matrix[i][k]
for j in range(k, n + 1):
matrix[i][j] -= d * matrix[k][j]
for row in matrix:
v.append(row[-1])
return v
except Exception as e:
raise
def __calc_a(self, v):
""" A calculation
:param list v: v-values
:return list : a-values
"""
try:
return [
(v[i + 1] - v[i])
/ (6 * (self.ts[i + 1] - self.ts[i]))
for i in range(self.n)
]
except Exception as e:
raise
def __calc_b(self, v):
""" B calculation
:param list v: v-values
:return list : b-values
"""
try:
return [v[i] / 2.0 for i in range(self.n)]
except Exception as e:
raise
def __calc_c(self, v):
""" C calculation
:param list v: v-values
:return list : c-values
"""
try:
return [
(self.ds[i + 1] - self.ds[i]) / (self.ts[i + 1] - self.ts[i]) \
- (self.ts[i + 1] - self.ts[i]) * (2 * v[i] + v[i + 1]) / 6
for i in range(self.n)
]
except Exception as e:
raise
def __calc_d(self):
""" D calculation
:return list: c-values
"""
try:
return self.ds
except Exception as e:
raise
def __search_i(self, t):
""" Index searching
:param float t: t-value
:return int i: index
"""
i, j = 0, len(self.ts) - 1
try:
while i < j:
k = (i + j) // 2
if self.ts[k] < t:
i = k + 1
else:
j = k
if i > 0:
i -= 1
return i
except Exception as e:
raise
class Graph:
def __init__(self, xs_0, ys_0, zs_0, xs_1, ys_1, zs_1):
self.xs_0, self.ys_0, self.zs_0, self.xs_1, self.ys_1, self.zs_1 = xs_0, ys_0, zs_0, xs_1, ys_1, zs_1
def plot2d(self):
try:
plt.title("2-D Spline Interpolation in XY/XZ")
plt.scatter(
self.xs_1, self.ys_1, c = "g",
label = "interpolated points XY", marker = "+"
)
plt.scatter(
self.xs_0, self.ys_0, c = "r",
label = "given points XY"
)
plt.scatter(
self.xs_1, self.zs_1, c = "b",
label = "interpolated points XZ", marker = "+"
)
plt.scatter(
self.xs_0, self.zs_0, c = "k",
label = "given points XZ"
)
plt.xlabel("x")
plt.ylabel("y,z")
plt.legend(loc = 2)
plt.grid(color = "gray", linestyle = "--")
#plt.show()
#plt.savefig("spline_interpolation.png")
except Exception as e:
raise
def plot3d(self):
ax = plt.figure().add_subplot(projection='3d')
x = self.xs_1
y = self.ys_1
z = self.zs_1
ax.scatter(x, y, z, c='b', label='Interpolated points')
ax.scatter(X, Y, Z, c='r', label='Given points')
# Make legend, set axes limits and labels
ax.legend()
ax.set_xlim(min(X),max(X))
ax.set_ylim(min(Y),max(Y))
ax.set_zlim(min(Z),max(Z))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Customize the view angle so it's easier to see that the scatter points lie
# on the plane y=0
ax.view_init(elev=20., azim=-35)
plt.show()
if __name__ == '__main__':
# (N + 1) points
T,X,Y,Z = [],[],[],[]
fileName = './points_input.txt'
import csv
with open(fileName, 'r') as f:
reader = csv.reader(f)
point_data = list(reader)
for line in point_data:
X.append(float(line[0]))
Y.append(float(line[1]))
Z.append(float(line[2]))
print('X:', X)
print('Y:', Y)
print('Z:', Z)
n=0
for x in X:
T.append(n+1.0)
n += 1
print('T: ', T)
#T = [1.0,2.0,3.0,4.0,5.0,6.0]
#X = [0.0, 2.0, 3.0, 5.0, 7.0, 8.0]
#Y = [0.8, 2.8, 3.2, 1.9, 4.5, 2.5]
#Z = [-0.5, 1.8, 2.2, 0.9, 3.5, -1.5]
S = 0.1 # Step for interpolation
S_1 = 1 / S # Inverse of S
xs_g, ys_g, zs_g = [], [], [] # List for graph
try:
# 3-D spline interpolation
si = SplineInterpolation(T, X)
for t in [t / S_1 for t in range(int(T[0] / S), int(T[-1] / S) + 1)]:
x= si.interpolate(t)
#print("{:8.4f}, {:8.4f}".format(t, x))
xs_g.append(x)
si = SplineInterpolation(T, Y)
for t in [t / S_1 for t in range(int(T[0] / S), int(T[-1] / S) + 1)]:
y = si.interpolate(t)
#print("{:8.4f}, {:8.4f}".format(t, y))
ys_g.append(y)
si = SplineInterpolation(T, Z)
for t in [t / S_1 for t in range(int(T[0] / S), int(T[-1] / S) + 1)]:
z = si.interpolate(t)
#print("{:8.4f}, {:8.4f}".format(t, z))
zs_g.append(z)
# Write output to file
file_out = 'output_file.txt'
print('Writing output to ',file_out)
n=0
output = open(file_out, 'w')
for x in xs_g:
string=("G0 X{:8.4f} Y{:8.4f} Z{:8.4f}\n".format(xs_g[n], ys_g[n], zs_g[n]))
output.write(string)
n += 1
# Closing file
output.close()
# Graph drawing
g = Graph(X, Y, Z, xs_g, ys_g, zs_g)
g.plot2d()
g.plot3d()
except Exception as e:
traceback.print_exc()
sys.exit(1)The 'points_input.txt' for the example below:
[code]583.8160, 2785.3929, -80.0100,
569.5160, 2551.3630, -20.8590,
569.5160, 2551.3630, -534.4340,
569.5160, 2551.3630, -563.0960,
587.9240, 2551.3630, -562.6310,
602.8020, 2531.2934, -547.8260,
616.4620, 2550.4623, -563.0180,
630.8120, 2550.4623, -563.9780,
601.7700, 1631.0440, -563.0410,
586.6920, 1633.2648, -561.9940,
574.5840, 1656.0775, -546.8950,
560.3560, 1634.1061, -561.9290,
545.8120, 1634.7045, -562.6420,
575.0200, 2556.2819, -563.3090,
575.0200, 2556.2819, -543.9050, which gives me this output:
And the 'output_file.txt' content created:
G0 X583.8160 Y2785.3929 Z-80.0100
G0 X581.9705 Y2755.7769 Z-55.4991
G0 X580.1501 Y2726.5375 Z-32.1152
G0 X578.3801 Y2698.0512 Z-10.9853
G0 X576.6857 Y2670.6945 Z 6.7635
G0 X575.0920 Y2644.8440 Z 20.0042
G0 X573.6242 Y2620.8762 Z 27.6098
G0 X572.3075 Y2599.1676 Z 28.4534
G0 X571.1671 Y2580.0949 Z 21.4077
G0 X570.2282 Y2564.0345 Z 5.3460
G0 X569.5160 Y2551.3630 Z-20.8590
G0 X569.0447 Y2542.3144 Z-57.7799
G0 X568.7852 Y2536.5528 Z-103.7722
G0 X568.6972 Y2533.5994 Z-156.6372
G0 X568.7407 Y2532.9760 Z-214.1762
G0 X568.8756 Y2534.2037 Z-274.1904
G0 X569.0617 Y2536.8043 Z-334.4811
G0 X569.2589 Y2540.2990 Z-392.8496
G0 X569.4271 Y2544.2094 Z-447.0970
G0 X569.5262 Y2548.0569 Z-495.0248
G0 X569.5160 Y2551.3630 Z-534.4340
G0 X569.3714 Y2553.7511 Z-563.7128
G0 X569.1269 Y2555.2528 Z-583.5966
G0 X568.8320 Y2556.0013 Z-595.4073
G0 X568.5363 Y2556.1302 Z-600.4671
G0 X568.2892 Y2555.7728 Z-600.0982
G0 X568.1403 Y2555.0627 Z-595.6226
G0 X568.1390 Y2554.1332 Z-588.3625
G0 X568.3348 Y2553.1178 Z-579.6400
G0 X568.7773 Y2552.1499 Z-570.7771
G0 X569.5160 Y2551.3630 Z-563.0960
G0 X570.5842 Y2550.8590 Z-557.6393
G0 X571.9506 Y2550.6142 Z-554.3315
G0 X573.5678 Y2550.5734 Z-552.8176
G0 X575.3883 Y2550.6814 Z-552.7427
G0 X577.3646 Y2550.8830 Z-553.7517
G0 X579.4494 Y2551.1230 Z-555.4896
G0 X581.5952 Y2551.3462 Z-557.6015
G0 X583.7545 Y2551.4974 Z-559.7324
G0 X585.8800 Y2551.5214 Z-561.5272
G0 X587.9240 Y2551.3630 Z-562.6310
G0 X589.8486 Y2550.9707 Z-562.7790
G0 X591.6530 Y2550.3078 Z-562.0676
G0 X593.3460 Y2549.3412 Z-560.6834
G0 X594.9361 Y2548.0378 Z-558.8128
G0 X596.4320 Y2546.3645 Z-556.6426
G0 X597.8424 Y2544.2884 Z-554.3592
G0 X599.1760 Y2541.7762 Z-552.1493
G0 X600.4413 Y2538.7951 Z-550.1994
G0 X601.6471 Y2535.3118 Z-548.6961
G0 X602.8020 Y2531.2934 Z-547.8260
G0 X603.9177 Y2526.8028 Z-547.7237
G0 X605.0178 Y2522.2873 Z-548.3158
G0 X606.1291 Y2518.2901 Z-549.4772
G0 X607.2782 Y2515.3547 Z-551.0824
G0 X608.4918 Y2514.0242 Z-553.0061
G0 X609.7966 Y2514.8420 Z-555.1232
G0 X611.2194 Y2518.3514 Z-557.3082
G0 X612.7867 Y2525.0958 Z-559.4358
G0 X614.5254 Y2535.6183 Z-561.3809
G0 X616.4620 Y2550.4623 Z-563.0180
G0 X618.6015 Y2569.6655 Z-564.2510
G0 X620.8617 Y2591.2429 Z-565.1000
G0 X623.1386 Y2612.7039 Z-565.6142
G0 X625.3283 Y2631.5580 Z-565.8430
G0 X627.3268 Y2645.3144 Z-565.8355
G0 X629.0301 Y2651.4827 Z-565.6410
G0 X630.3342 Y2647.5723 Z-565.3088
G0 X631.1352 Y2631.0924 Z-564.8881
G0 X631.3291 Y2599.5526 Z-564.4280
G0 X630.8120 Y2550.4623 Z-563.9780
G0 X629.5179 Y2482.4155 Z-563.5794
G0 X627.5335 Y2398.3451 Z-563.2423
G0 X624.9835 Y2302.2688 Z-562.9691
G0 X621.9925 Y2198.2040 Z-562.7621
G0 X618.6853 Y2090.1684 Z-562.6236
G0 X615.1865 Y1982.1797 Z-562.5561
G0 X611.6209 Y1878.2552 Z-562.5617
G0 X608.1131 Y1782.4128 Z-562.6428
G0 X604.7879 Y1698.6698 Z-562.8018
G0 X601.7700 Y1631.0440 Z-563.0410
G0 X599.1548 Y1582.4611 Z-563.3543
G0 X596.9208 Y1551.4794 Z-563.7023
G0 X595.0174 Y1535.5657 Z-564.0372
G0 X593.3939 Y1532.1864 Z-564.3110
G0 X591.9996 Y1538.8083 Z-564.4760
G0 X590.7838 Y1552.8978 Z-564.4844
G0 X589.6959 Y1571.9216 Z-564.2881
G0 X588.6850 Y1593.3463 Z-563.8396
G0 X587.7006 Y1614.6385 Z-563.0908
G0 X586.6920 Y1633.2648 Z-561.9940
G0 X585.6189 Y1647.2323 Z-560.5268
G0 X584.4829 Y1656.7102 Z-558.7692
G0 X583.2962 Y1662.4082 Z-556.8264
G0 X582.0709 Y1665.0362 Z-554.8039
G0 X580.8189 Y1665.3038 Z-552.8070
G0 X579.5525 Y1663.9208 Z-550.9411
G0 X578.2837 Y1661.5969 Z-549.3115
G0 X577.0247 Y1659.0419 Z-548.0238
G0 X575.7874 Y1656.9655 Z-547.1831
G0 X574.5840 Y1656.0775 Z-546.8950
G0 X573.4199 Y1656.8530 Z-547.2291
G0 X572.2735 Y1658.8288 Z-548.1125
G0 X571.1167 Y1661.3070 Z-549.4367
G0 X569.9212 Y1663.5899 Z-551.0932
G0 X568.6588 Y1664.9796 Z-552.9732
G0 X567.3014 Y1664.7782 Z-554.9684
G0 X565.8206 Y1662.2880 Z-556.9701
G0 X564.1882 Y1656.8112 Z-558.8699
G0 X562.3761 Y1647.6498 Z-560.5590
G0 X560.3560 Y1634.1061 Z-561.9290
G0 X558.1230 Y1616.0128 Z-562.8998
G0 X555.7654 Y1595.3251 Z-563.5050
G0 X553.3949 Y1574.5286 Z-563.8068
G0 X551.1229 Y1556.1090 Z-563.8672
G0 X549.0612 Y1542.5520 Z-563.7486
G0 X547.3213 Y1536.3432 Z-563.5128
G0 X546.0148 Y1539.9684 Z-563.2222
G0 X545.2534 Y1555.9132 Z-562.9387
G0 X545.1486 Y1586.6634 Z-562.7246
G0 X545.8120 Y1634.7045 Z-562.6420
G0 X547.3111 Y1701.4656 Z-562.7336
G0 X549.5362 Y1784.1490 Z-562.9644
G0 X552.3336 Y1878.9001 Z-563.2803
G0 X555.5494 Y1981.8646 Z-563.6268
G0 X559.0300 Y2089.1879 Z-563.9497
G0 X562.6214 Y2197.0156 Z-564.1946
G0 X566.1699 Y2301.4934 Z-564.3073
G0 X569.5217 Y2398.7666 Z-564.2335
G0 X572.5230 Y2484.9810 Z-563.9188
G0 X575.0200 Y2556.2819 Z-563.3090
G0 X576.8955 Y2609.7702 Z-562.3646
G0 X578.1788 Y2646.3675 Z-561.1056
G0 X578.9356 Y2667.9505 Z-559.5671
G0 X579.2317 Y2676.3960 Z-557.7840
G0 X579.1330 Y2673.5808 Z-555.7912
G0 X578.7053 Y2661.3818 Z-553.6236
G0 X578.0143 Y2641.6755 Z-551.3163
G0 X577.1259 Y2616.3390 Z-548.9041
G0 X576.1058 Y2587.2488 Z-546.4220
G0 X575.0200 Y2556.2819 Z-543.9050Attachments:
Please Log in or Create an account to join the conversation.
10 Oct 2024 15:56 - 10 Oct 2024 15:56 #311748
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
Just as an explanation.
The script basically calculates a spline for each axis separately (ie one of X, one for Y and one for Z). The resulting 3D curve is the combination of the individual x,y,z values at a given iteration index (t):
The script basically calculates a spline for each axis separately (ie one of X, one for Y and one for Z). The resulting 3D curve is the combination of the individual x,y,z values at a given iteration index (t):
Attachments:
Please Log in or Create an account to join the conversation.
Time to create page: 0.085 seconds