- GCode and Part Programs
- O Codes (subroutines) and NGCGUI
- Remap 3D Cubic Spline Interpolation code by Python
Remap 3D Cubic Spline Interpolation code by Python
- jurod
-
 Topic Author
Topic Author
- Offline
- Senior Member
-

Less
More
- Posts: 68
- Thank you received: 6
19 Sep 2024 11:01 #310440
by jurod
Remap 3D Cubic Spline Interpolation code by Python was created by jurod
Hi, I don't know how to create something functional. My idea is as follows:
Create a Gcod remap for example G5.4/5.5 (start and end of block in gcode)
Using the project from BigJohnT from this page forum.linuxcnc.org/21-axis/30986-axis-position-logger?start=100
After creating the gcode, I would like to easily edit this code to spline using the remap code.
Original from position Logger:Edited:From site stackoverflow.com/questions/31543775/how...on/48085583#48085583
Example Python cede:[/code]
I'm not a python programmer. Is it possible to make something similar work?
Create a Gcod remap for example G5.4/5.5 (start and end of block in gcode)
Using the project from BigJohnT from this page forum.linuxcnc.org/21-axis/30986-axis-position-logger?start=100
After creating the gcode, I would like to easily edit this code to spline using the remap code.
Original from position Logger:
G40 G80 G98
M6 T1 G43
S 20000 M3
G1 Z-100.0 F5000
G1 X583.8160 Y2785.3929 Z-80.0100 B-0.0060 C-180.6420
G1 X569.5160 Y2551.3630 Z-20.8590 B-0.0060 C-180.6420
G1 X569.5160 Y2551.3630 Z-534.4340 B-0.0060 C-180.6420
G1 X569.5160 Y2551.3630 Z-563.0960 B-0.0060 C-180.6420
G1 X587.9240 Y2551.3630 Z-562.6310 B-0.0060 C-180.6420
G1 X602.8020 Y2531.2934 Z-547.8260 B-0.0060 C-180.6420
G1 X616.4620 Y2550.4623 Z-563.0180 B-0.0060 C-180.6420
G1 X630.8120 Y2550.4623 Z-563.9780 B-0.0060 C-180.6420
G1 X601.7700 Y1631.0440 Z-563.0410 B-0.0060 C-180.6420
G1 X586.6920 Y1633.2648 Z-561.9940 B-0.0060 C-180.6420
G1 X574.5840 Y1656.0775 Z-546.8950 B-0.0060 C-180.6420
G1 X560.3560 Y1634.1061 Z-561.9290 B-0.0060 C-180.6420
G1 X545.8120 Y1634.7045 Z-562.6420 B-0.0060 C-180.6420
G1 X575.0200 Y2556.2819 Z-563.3090 B-0.0060 C-180.6420
G1 X575.0200 Y2556.2819 Z-543.9050 B-0.0060 C-180.6420
;
G1 Z-100.0 F20000
G1 X583.8160 Y2785.3929 Z-80.0100 B-0.0060 C-180.6420
M2G40 G80 G98
M6 T1 G43
S 20000 M3
G1 Z-100.0 F5000
G5.4 X583.8160 Y2785.3929 Z-80.0100 B-0.0060 C-180.6420
X569.5160 Y2551.3630 Z-20.8590 B-0.0060 C-180.6420
X569.5160 Y2551.3630 Z-534.4340 B-0.0060 C-180.6420
X569.5160 Y2551.3630 Z-563.0960 B-0.0060 C-180.6420
X587.9240 Y2551.3630 Z-562.6310 B-0.0060 C-180.6420
X602.8020 Y2531.2934 Z-547.8260 B-0.0060 C-180.6420
X616.4620 Y2550.4623 Z-563.0180 B-0.0060 C-180.6420
X630.8120 Y2550.4623 Z-563.9780 B-0.0060 C-180.6420
X601.7700 Y1631.0440 Z-563.0410 B-0.0060 C-180.6420
X586.6920 Y1633.2648 Z-561.9940 B-0.0060 C-180.6420
X574.5840 Y1656.0775 Z-546.8950 B-0.0060 C-180.6420
X560.3560 Y1634.1061 Z-561.9290 B-0.0060 C-180.6420
X545.8120 Y1634.7045 Z-562.6420 B-0.0060 C-180.6420
X575.0200 Y2556.2819 Z-563.3090 B-0.0060 C-180.6420
G5.5 X575.0200 Y2556.2819 Z-543.9050 B-0.0060 C-180.6420
;
G1 Z-100.0 F20000
G1 X583.8160 Y2785.3929 Z-80.0100 B-0.0060 C-180.6420
M2Example Python cede:
[code]def my_cubic_interp1d(x0, x, y):
"""
Interpolate a 1-D function using cubic splines.
x0 : a 1d-array of floats to interpolate at
x : a 1-D array of floats sorted in increasing order
y : A 1-D array of floats. The length of y along the
interpolation axis must be equal to the length of x.
Implement a trick to generate at first step the cholesky matrice L of
the tridiagonal matrice A (thus L is a bidiagonal matrice that
can be solved in two distinct loops).
additional ref: www.math.uh.edu/~jingqiu/math4364/spline.pdf
# original function code at: https://stackoverflow.com/a/48085583/36061
This function is licenced under: Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
https://creativecommons.org/licenses/by-sa/3.0/
Original Author raphael valentin
Date 3 Jan 2018
Modifications made to remove numpy dependencies:
-all sub-functions by MR
This function, and all sub-functions, are licenced under: Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
Mod author: Matthew Rowles
Date 3 May 2021
"""
def diff(lst):
"""
numpy.diff with default settings
"""
size = len(lst)-1
r = [0]*size
for i in range(size):
r[i] = lst[i+1] - lst[i]
return r
def list_searchsorted(listToInsert, insertInto):
"""
numpy.searchsorted with default settings
"""
def float_searchsorted(floatToInsert, insertInto):
for i in range(len(insertInto)):
if floatToInsert <= insertInto[i]:
return i
return len(insertInto)
return [float_searchsorted(i, insertInto) for i in listToInsert]
def clip(lst, min_val, max_val, inPlace = False):
"""
numpy.clip
"""
if not inPlace:
lst = lst[:]
for i in range(len(lst)):
if lst[i] < min_val:
lst[i] = min_val
elif lst[i] > max_val:
lst[i] = max_val
return lst
def subtract(a,b):
"""
returns a - b
"""
return a - b
size = len(x)
xdiff = diff(x)
ydiff = diff(y)
# allocate buffer matrices
Li = [0]*size
Li_1 = [0]*(size-1)
z = [0]*(size)
# fill diagonals Li and Li-1 and solve [L][y] = [B]
Li[0] = sqrt(2*xdiff[0])
Li_1[0] = 0.0
B0 = 0.0 # natural boundary
z[0] = B0 / Li[0]
for i in range(1, size-1, 1):
Li_1[i] = xdiff[i-1] / Li[i-1]
Li[i] = sqrt(2*(xdiff[i-1]+xdiff[i]) - Li_1[i-1] * Li_1[i-1])
Bi = 6*(ydiff[i]/xdiff[i] - ydiff[i-1]/xdiff[i-1])
z[i] = (Bi - Li_1[i-1]*z[i-1])/Li[i]
i = size - 1
Li_1[i-1] = xdiff[-1] / Li[i-1]
Li[i] = sqrt(2*xdiff[-1] - Li_1[i-1] * Li_1[i-1])
Bi = 0.0 # natural boundary
z[i] = (Bi - Li_1[i-1]*z[i-1])/Li[i]
# solve [L.T][x] = [y]
i = size-1
z[i] = z[i] / Li[i]
for i in range(size-2, -1, -1):
z[i] = (z[i] - Li_1[i-1]*z[i+1])/Li[i]
# find index
index = list_searchsorted(x0,x)
index = clip(index, 1, size-1)
xi1 = [x[num] for num in index]
xi0 = [x[num-1] for num in index]
yi1 = [y[num] for num in index]
yi0 = [y[num-1] for num in index]
zi1 = [z[num] for num in index]
zi0 = [z[num-1] for num in index]
hi1 = list( map(subtract, xi1, xi0) )
# calculate cubic - all element-wise multiplication
f0 = [0]*len(hi1)
for j in range(len(f0)):
f0[j] = zi0[j]/(6*hi1[j])*(xi1[j]-x0[j])**3 + \
zi1[j]/(6*hi1[j])*(x0[j]-xi0[j])**3 + \
(yi1[j]/hi1[j] - zi1[j]*hi1[j]/6)*(x0[j]-xi0[j]) + \
(yi0[j]/hi1[j] - zi0[j]*hi1[j]/6)*(xi1[j]-x0[j])
return f0I'm not a python programmer. Is it possible to make something similar work?
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
19 Sep 2024 15:08 - 19 Sep 2024 15:53 #310461
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
I cannot comment on the example python code.
A python remap can certainly parse a file of logged point coordinates, do calculations on those points and then output the results as, say, a list of G1 X.. Y.. Z.. moves and write these into a ngc subroutine that is called later in the gcode.
The issue with python is the time it takes to do all these things so if you expect to be able to do something like this:
G01 X.. Y.. Z.. F...
G5.4 ...
and expect this to blend without pause then that is likely not possible because of the lag inherent to python. However if you can pause gcode execution for the time it takes the python script to do its thing then I don't see a problem.
In a python remap controlling the read-ahead is VERY important. The first thing you want to do is stop the read-ahead before it ingests the python remap. Hence there won't be any blending between the Gcode before the remap and the remap itself.
A python remap can certainly parse a file of logged point coordinates, do calculations on those points and then output the results as, say, a list of G1 X.. Y.. Z.. moves and write these into a ngc subroutine that is called later in the gcode.
The issue with python is the time it takes to do all these things so if you expect to be able to do something like this:
G01 X.. Y.. Z.. F...
G5.4 ...
and expect this to blend without pause then that is likely not possible because of the lag inherent to python. However if you can pause gcode execution for the time it takes the python script to do its thing then I don't see a problem.
In a python remap controlling the read-ahead is VERY important. The first thing you want to do is stop the read-ahead before it ingests the python remap. Hence there won't be any blending between the Gcode before the remap and the remap itself.
Last edit: 19 Sep 2024 15:53 by Aciera.
Please Log in or Create an account to join the conversation.
- Todd Zuercher
-

- Away
- Platinum Member
-

Less
More
- Posts: 4704
- Thank you received: 1443
19 Sep 2024 17:36 #310467
by Todd Zuercher
Replied by Todd Zuercher on topic Remap 3D Cubic Spline Interpolation code by Python
I don't think the way to do this is with a g-code remap. Seems to me it should be job of a file filter that reads and translates the g-code file on loading. That is perfectly acceptable as a python script, or even a bash sed script. Then the time to process is only at file loading and it doesn't get in the way of the running realtime code.
Please Log in or Create an account to join the conversation.
- jurod
-
 Topic Author
Topic Author
- Offline
- Senior Member
-

Less
More
- Posts: 68
- Thank you received: 6
20 Sep 2024 09:01 #310502
by jurod
Replied by jurod on topic Remap 3D Cubic Spline Interpolation code by Python
You are probably right. I didn't realize the delay in the code, but that's not a bug. It can be a few seconds.
The method according to Todd is also a solution.
I'm not sure which way to go.
I don't know how to work well in Python (only a couple of basic simple things and editing)
Is there anyone who would help me with this problem?
The method according to Todd is also a solution.
I'm not sure which way to go.
I don't know how to work well in Python (only a couple of basic simple things and editing)
Is there anyone who would help me with this problem?
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
20 Sep 2024 10:46 - 20 Sep 2024 10:47 #310503
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
If you don't need to log the points and calculate the interpolation in the same gcode then a filter is likely easier. The other thing is that your python script is for a planar curve (eg XY) but you want to interpolate in 3D. I'm not familiar with cubic interpolation for a 3d curve so I'm not sure if it would require interpolating XY and XZ separately and then combine the two.
If you had a clear description of how to calculate the way points for the interpolated curve (even if it's just in words) I might be able to put something together but I don't have the time to research the math right now.
If you had a clear description of how to calculate the way points for the interpolated curve (even if it's just in words) I might be able to put something together but I don't have the time to research the math right now.
Last edit: 20 Sep 2024 10:47 by Aciera.
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
20 Sep 2024 10:56 #310504
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
There was a fairly long discussion about 3d splines/clothoids here:
forum.linuxcnc.org/38-general-linuxcnc-q...lib?start=500#305223
forum.linuxcnc.org/38-general-linuxcnc-q...lib?start=500#305223
Please Log in or Create an account to join the conversation.
- jurod
-
 Topic Author
Topic Author
- Offline
- Senior Member
-

Less
More
- Posts: 68
- Thank you received: 6
10 Oct 2024 08:38 #311711
by jurod
Replied by jurod on topic Remap 3D Cubic Spline Interpolation code by Python
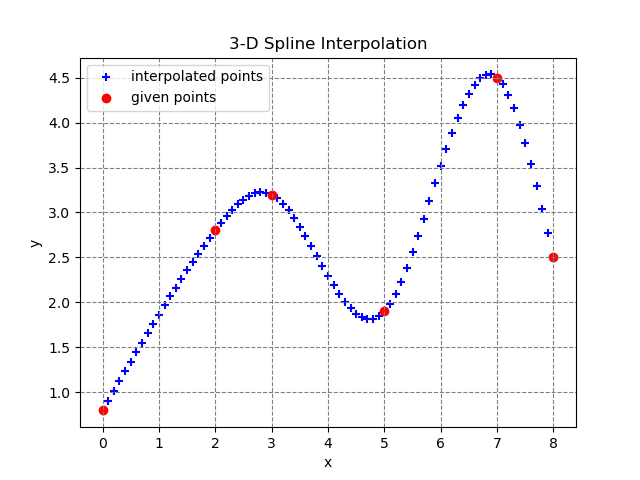
This code should be correct on a 3d spline
#! /usr/local/bin/python3.6
"""
3-D spline interpolation
(with graph drawing by matplotlib)
"""
import matplotlib.pyplot as plt
import sys
import traceback
class SplineInterpolation:
def __init__(self, xs, ys):
""" Initialization
:param list xs: x-coordinate list of given points
:param list ys: y-coordinate list of given points
"""
self.xs, self.ys = xs, ys
self.n = len(self.xs) - 1
h = self.__calc_h()
w = self.__calc_w(h)
matrix = self.__gen_matrix(h, w)
v = [0] + self.__gauss_jordan(matrix) + [0]
self.b = self.__calc_b(v)
self.a = self.__calc_a(v)
self.d = self.__calc_d()
self.c = self.__calc_c(v)
def interpolate(self, t):
""" Interpolation
:param float t: x-value for a interpolate target
:return float : computated y-value
"""
try:
i = self.__search_i(t)
return self.a[i] * (t - self.xs[i]) ** 3 \
+ self.b[i] * (t - self.xs[i]) ** 2 \
+ self.c[i] * (t - self.xs[i]) \
+ self.d[i]
except Exception as e:
raise
def __calc_h(self):
""" H calculation
:return list: h-values
"""
try:
return [self.xs[i + 1] - self.xs[i] for i in range(self.n)]
except Exception as e:
raise
def __calc_w(self, h):
""" W calculation
:param list h: h-values
:return list : w-values
"""
try:
return [
6 * ((self.ys[i + 1] - self.ys[i]) / h[i]
- (self.ys[i] - self.ys[i - 1]) / h[i - 1])
for i in range(1, self.n)
]
except Exception as e:
raise
def __gen_matrix(self, h, w):
""" Matrix generation
:param list h: h-values
:param list w: w-values
:return list mtx: generated 2-D matrix
"""
mtx = [[0 for _ in range(self.n)] for _ in range(self.n - 1)]
try:
for i in range(self.n - 1):
mtx[i][i] = 2 * (h[i] + h[i + 1])
mtx[i][-1] = w[i]
if i == 0:
continue
mtx[i - 1][i] = h[i]
mtx[i][i - 1] = h[i]
return mtx
except Exception as e:
raise
def __gauss_jordan(self, matrix):
""" Solving of simultaneous linear equations
with Gauss-Jordan's method
:param list mtx: list of 2-D matrix
:return list v: answers list of simultaneous linear equations
"""
v = []
n = self.n - 1
try:
for k in range(n):
p = matrix[k][k]
for j in range(k, n + 1):
matrix[k][j] /= p
for i in range(n):
if i == k:
continue
d = matrix[i][k]
for j in range(k, n + 1):
matrix[i][j] -= d * matrix[k][j]
for row in matrix:
v.append(row[-1])
return v
except Exception as e:
raise
def __calc_a(self, v):
""" A calculation
:param list v: v-values
:return list : a-values
"""
try:
return [
(v[i + 1] - v[i])
/ (6 * (self.xs[i + 1] - self.xs[i]))
for i in range(self.n)
]
except Exception as e:
raise
def __calc_b(self, v):
""" B calculation
:param list v: v-values
:return list : b-values
"""
try:
return [v[i] / 2.0 for i in range(self.n)]
except Exception as e:
raise
def __calc_c(self, v):
""" C calculation
:param list v: v-values
:return list : c-values
"""
try:
return [
(self.ys[i + 1] - self.ys[i]) / (self.xs[i + 1] - self.xs[i]) \
- (self.xs[i + 1] - self.xs[i]) * (2 * v[i] + v[i + 1]) / 6
for i in range(self.n)
]
except Exception as e:
raise
def __calc_d(self):
""" D calculation
:return list: c-values
"""
try:
return self.ys
except Exception as e:
raise
def __search_i(self, t):
""" Index searching
:param float t: t-value
:return int i: index
"""
i, j = 0, len(self.xs) - 1
try:
while i < j:
k = (i + j) // 2
if self.xs[k] < t:
i = k + 1
else:
j = k
if i > 0:
i -= 1
return i
except Exception as e:
raise
class Graph:
def __init__(self, xs_0, ys_0, xs_1, ys_1):
self.xs_0, self.ys_0, self.xs_1, self.ys_1 = xs_0, ys_0, xs_1, ys_1
def plot(self):
""" Graph plotting """
try:
plt.title("3-D Spline Interpolation")
plt.scatter(
self.xs_1, self.ys_1, c = "b",
label = "interpolated points", marker = "+"
)
plt.scatter(
self.xs_0, self.ys_0, c = "r",
label = "given points"
)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc = 2)
plt.grid(color = "gray", linestyle = "--")
#plt.show()
plt.savefig("spline_interpolation.png")
except Exception as e:
raise
if __name__ == '__main__':
# (N + 1) points
X = [0.0, 2.0, 3.0, 5.0, 7.0, 8.0]
Y = [0.8, 2.8, 3.2, 1.9, 4.5, 2.5]
S = 0.1 # Step for interpolation
S_1 = 1 / S # Inverse of S
xs_g, ys_g = [], [] # List for graph
try:
# 3-D spline interpolation
si = SplineInterpolation(X, Y)
for x in [x / S_1 for x in range(int(X[0] / S), int(X[-1] / S) + 1)]:
y = si.interpolate(x)
print("{:8.4f}, {:8.4f}".format(x, y))
xs_g.append(x)
ys_g.append(y)
# Graph drawing
g = Graph(X, Y, xs_g, ys_g)
g.plot()
except Exception as e:
traceback.print_exc()
sys.exit(1)Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
10 Oct 2024 09:03 - 10 Oct 2024 09:25 #311714
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
Attachments:
Last edit: 10 Oct 2024 09:25 by Aciera.
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
10 Oct 2024 12:26 #311722
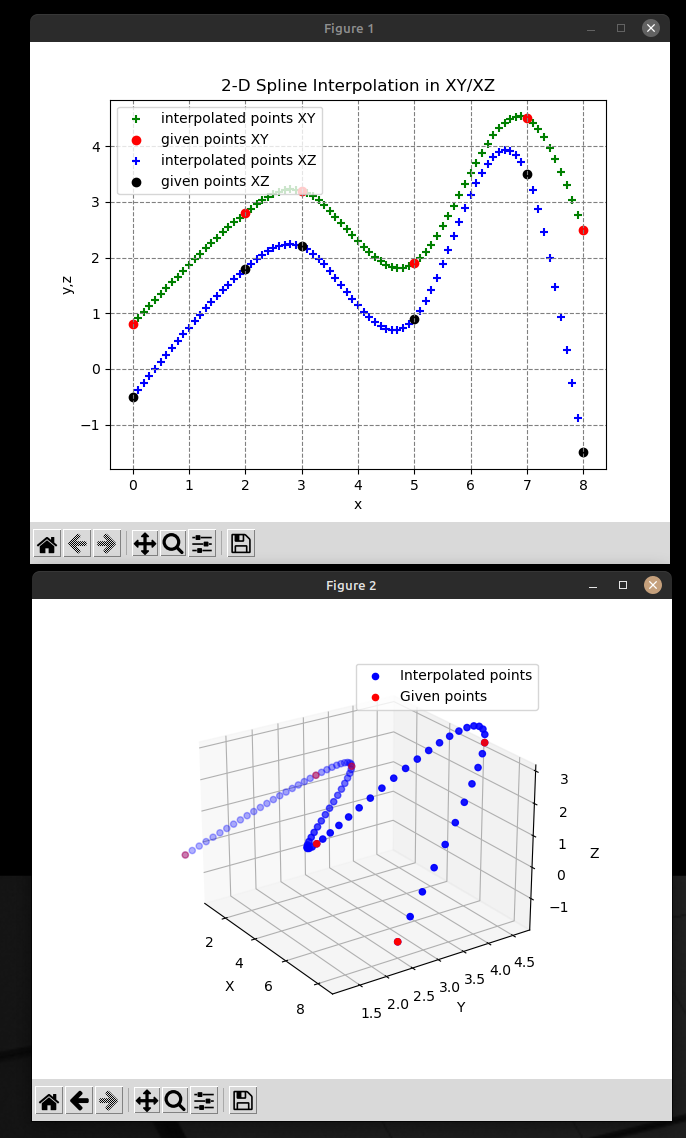
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
Your code sample expanded to 3D:
gives me this:
Which looks ok.
#! /usr/local/bin/python3.6
"""
3-D spline interpolation
(with graph drawing by matplotlib)
"""
import matplotlib.pyplot as plt
import sys
import traceback
class SplineInterpolation_xy:
def __init__(self, xs, ys):
""" Initialization
:param list xs: x-coordinate list of given points
:param list ys: y-coordinate list of given points
"""
self.xs, self.ys = xs, ys
self.n = len(self.xs) - 1
h = self.__calc_h()
w = self.__calc_w(h)
matrix = self.__gen_matrix(h, w)
v = [0] + self.__gauss_jordan(matrix) + [0]
self.b = self.__calc_b(v)
self.a = self.__calc_a(v)
self.d = self.__calc_d()
self.c = self.__calc_c(v)
def interpolate(self, t):
""" Interpolation
:param float t: x-value for a interpolate target
:return float : computated y-value
"""
try:
i = self.__search_i(t)
return self.a[i] * (t - self.xs[i]) ** 3 \
+ self.b[i] * (t - self.xs[i]) ** 2 \
+ self.c[i] * (t - self.xs[i]) \
+ self.d[i]
except Exception as e:
raise
def __calc_h(self):
""" H calculation
:return list: h-values
"""
try:
return [self.xs[i + 1] - self.xs[i] for i in range(self.n)]
except Exception as e:
raise
def __calc_w(self, h):
""" W calculation
:param list h: h-values
:return list : w-values
"""
try:
return [
6 * ((self.ys[i + 1] - self.ys[i]) / h[i]
- (self.ys[i] - self.ys[i - 1]) / h[i - 1])
for i in range(1, self.n)
]
except Exception as e:
raise
def __gen_matrix(self, h, w):
""" Matrix generation
:param list h: h-values
:param list w: w-values
:return list mtx: generated 2-D matrix
"""
mtx = [[0 for _ in range(self.n)] for _ in range(self.n - 1)]
try:
for i in range(self.n - 1):
mtx[i][i] = 2 * (h[i] + h[i + 1])
mtx[i][-1] = w[i]
if i == 0:
continue
mtx[i - 1][i] = h[i]
mtx[i][i - 1] = h[i]
return mtx
except Exception as e:
raise
def __gauss_jordan(self, matrix):
""" Solving of simultaneous linear equations
with Gauss-Jordan's method
:param list mtx: list of 2-D matrix
:return list v: answers list of simultaneous linear equations
"""
v = []
n = self.n - 1
try:
for k in range(n):
p = matrix[k][k]
for j in range(k, n + 1):
matrix[k][j] /= p
for i in range(n):
if i == k:
continue
d = matrix[i][k]
for j in range(k, n + 1):
matrix[i][j] -= d * matrix[k][j]
for row in matrix:
v.append(row[-1])
return v
except Exception as e:
raise
def __calc_a(self, v):
""" A calculation
:param list v: v-values
:return list : a-values
"""
try:
return [
(v[i + 1] - v[i])
/ (6 * (self.xs[i + 1] - self.xs[i]))
for i in range(self.n)
]
except Exception as e:
raise
def __calc_b(self, v):
""" B calculation
:param list v: v-values
:return list : b-values
"""
try:
return [v[i] / 2.0 for i in range(self.n)]
except Exception as e:
raise
def __calc_c(self, v):
""" C calculation
:param list v: v-values
:return list : c-values
"""
try:
return [
(self.ys[i + 1] - self.ys[i]) / (self.xs[i + 1] - self.xs[i]) \
- (self.xs[i + 1] - self.xs[i]) * (2 * v[i] + v[i + 1]) / 6
for i in range(self.n)
]
except Exception as e:
raise
def __calc_d(self):
""" D calculation
:return list: c-values
"""
try:
return self.ys
except Exception as e:
raise
def __search_i(self, t):
""" Index searching
:param float t: t-value
:return int i: index
"""
i, j = 0, len(self.xs) - 1
try:
while i < j:
k = (i + j) // 2
if self.xs[k] < t:
i = k + 1
else:
j = k
if i > 0:
i -= 1
return i
except Exception as e:
raise
class SplineInterpolation_xz:
def __init__(self, xs, zs):
""" Initialization
:param list xs: x-coordinate list of given points
:param list zs: z-coordinate list of given points
"""
self.xs, self.zs = xs, zs
self.n = len(self.xs) - 1
h = self.__calc_h()
w = self.__calc_w(h)
matrix = self.__gen_matrix(h, w)
v = [0] + self.__gauss_jordan(matrix) + [0]
self.b = self.__calc_b(v)
self.a = self.__calc_a(v)
self.d = self.__calc_d()
self.c = self.__calc_c(v)
def interpolate(self, t):
""" Interpolation
:param float t: x-value for a interpolate target
:return float : computated y-value
"""
try:
i = self.__search_i(t)
return self.a[i] * (t - self.xs[i]) ** 3 \
+ self.b[i] * (t - self.xs[i]) ** 2 \
+ self.c[i] * (t - self.xs[i]) \
+ self.d[i]
except Exception as e:
raise
def __calc_h(self):
""" H calculation
:return list: h-values
"""
try:
return [self.xs[i + 1] - self.xs[i] for i in range(self.n)]
except Exception as e:
raise
def __calc_w(self, h):
""" W calculation
:param list h: h-values
:return list : w-values
"""
try:
return [
6 * ((self.zs[i + 1] - self.zs[i]) / h[i]
- (self.zs[i] - self.zs[i - 1]) / h[i - 1])
for i in range(1, self.n)
]
except Exception as e:
raise
def __gen_matrix(self, h, w):
""" Matrix generation
:param list h: h-values
:param list w: w-values
:return list mtx: generated 2-D matrix
"""
mtx = [[0 for _ in range(self.n)] for _ in range(self.n - 1)]
try:
for i in range(self.n - 1):
mtx[i][i] = 2 * (h[i] + h[i + 1])
mtx[i][-1] = w[i]
if i == 0:
continue
mtx[i - 1][i] = h[i]
mtx[i][i - 1] = h[i]
return mtx
except Exception as e:
raise
def __gauss_jordan(self, matrix):
""" Solving of simultaneous linear equations
with Gauss-Jordan's method
:param list mtx: list of 2-D matrix
:return list v: answers list of simultaneous linear equations
"""
v = []
n = self.n - 1
try:
for k in range(n):
p = matrix[k][k]
for j in range(k, n + 1):
matrix[k][j] /= p
for i in range(n):
if i == k:
continue
d = matrix[i][k]
for j in range(k, n + 1):
matrix[i][j] -= d * matrix[k][j]
for row in matrix:
v.append(row[-1])
return v
except Exception as e:
raise
def __calc_a(self, v):
""" A calculation
:param list v: v-values
:return list : a-values
"""
try:
return [
(v[i + 1] - v[i])
/ (6 * (self.xs[i + 1] - self.xs[i]))
for i in range(self.n)
]
except Exception as e:
raise
def __calc_b(self, v):
""" B calculation
:param list v: v-values
:return list : b-values
"""
try:
return [v[i] / 2.0 for i in range(self.n)]
except Exception as e:
raise
def __calc_c(self, v):
""" C calculation
:param list v: v-values
:return list : c-values
"""
try:
return [
(self.zs[i + 1] - self.zs[i]) / (self.xs[i + 1] - self.xs[i]) \
- (self.xs[i + 1] - self.xs[i]) * (2 * v[i] + v[i + 1]) / 6
for i in range(self.n)
]
except Exception as e:
raise
def __calc_d(self):
""" D calculation
:return list: c-values
"""
try:
return self.zs
except Exception as e:
raise
def __search_i(self, t):
""" Index searching
:param float t: t-value
:return int i: index
"""
i, j = 0, len(self.xs) - 1
try:
while i < j:
k = (i + j) // 2
if self.xs[k] < t:
i = k + 1
else:
j = k
if i > 0:
i -= 1
return i
except Exception as e:
raise
class Graph:
def __init__(self, xs_0, ys_0, zs_0, xs_1, ys_1, zs_1):
self.xs_0, self.ys_0, self.zs_0, self.xs_1, self.ys_1, self.zs_1 = xs_0, ys_0, zs_0, xs_1, ys_1, zs_1
def plot2d(self):
try:
plt.title("2-D Spline Interpolation in XY/XZ")
plt.scatter(
self.xs_1, self.ys_1, c = "g",
label = "interpolated points XY", marker = "+"
)
plt.scatter(
self.xs_0, self.ys_0, c = "r",
label = "given points XY"
)
plt.scatter(
self.xs_1, self.zs_1, c = "b",
label = "interpolated points XZ", marker = "+"
)
plt.scatter(
self.xs_0, self.zs_0, c = "k",
label = "given points XZ"
)
plt.xlabel("x")
plt.ylabel("y,z")
plt.legend(loc = 2)
plt.grid(color = "gray", linestyle = "--")
#plt.show()
#plt.savefig("spline_interpolation.png")
except Exception as e:
raise
def plot3d(self):
ax = plt.figure().add_subplot(projection='3d')
x = self.xs_1
y = self.ys_1
z = self.zs_1
ax.scatter(x, y, z, c='b', label='Interpolated points')
ax.scatter(X, Y, Z, c='r', label='Given points')
# Make legend, set axes limits and labels
ax.legend()
ax.set_xlim(min(X),max(X))
ax.set_ylim(min(Y),max(Y))
ax.set_zlim(min(Z),max(Z))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Customize the view angle so it's easier to see that the scatter points lie
# on the plane y=0
ax.view_init(elev=20., azim=-35)
plt.show()
if __name__ == '__main__':
# (N + 1) points
X = [0.0, 2.0, 3.0, 5.0, 7.0, 8.0]
Y = [0.8, 2.8, 3.2, 1.9, 4.5, 2.5]
Z = [-0.5, 1.8, 2.2, 0.9, 3.5, -1.5]
S = 0.1 # Step for interpolation
S_1 = 1 / S # Inverse of S
xs_g, ys_g, zs_g = [], [], [] # List for graph
try:
# 3-D spline interpolation
si = SplineInterpolation_xy(X, Y)
for x in [x / S_1 for x in range(int(X[0] / S), int(X[-1] / S) + 1)]:
y = si.interpolate(x)
print("{:8.4f}, {:8.4f}".format(x, y))
xs_g.append(x)
ys_g.append(y)
si = SplineInterpolation_xz(X, Z)
for x in [x / S_1 for x in range(int(X[0] / S), int(X[-1] / S) + 1)]:
z = si.interpolate(x)
print("{:8.4f}, {:8.4f}".format(x, z))
zs_g.append(z)
# Graph drawing
print('Graph...')
g = Graph(X, Y, Z, xs_g, ys_g, zs_g)
g.plot2d()
g.plot3d()
except Exception as e:
traceback.print_exc()
sys.exit(1)gives me this:
Which looks ok.
Attachments:
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
10 Oct 2024 12:42 - 10 Oct 2024 13:22 #311723
by Aciera
Replied by Aciera on topic Remap 3D Cubic Spline Interpolation code by Python
Note that the interpolation code can only handle point lists with increasing X coordinate values.
Attachments:
Last edit: 10 Oct 2024 13:22 by Aciera.
Please Log in or Create an account to join the conversation.
- GCode and Part Programs
- O Codes (subroutines) and NGCGUI
- Remap 3D Cubic Spline Interpolation code by Python
Time to create page: 0.137 seconds