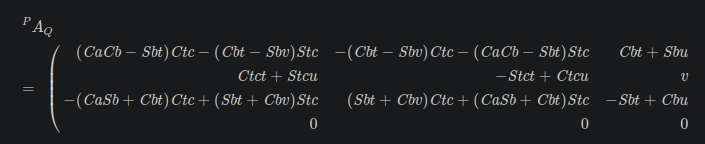Kinematic model for a 5axis mill with universal (nutating) head

Do I have to use decimal numbers or is there any other solutions?

I would first try using the exact algebraic expression (ie sin(50°), cos(50°)) and see what the rotation matrix looks like.

This is what I came up with 

If you manage to get the correct forward and inverse kinematic model using pen and paper then my hat is definitely going to be off to you. I started out that way ...
I attach my jupyter notebook (remove the '.txt') which contains all the ipython symbolic math to automatically derive all the formulas in the documentation. Using jupyter and ipython will save you a LOT of paper and headache.
You will need to adjust some of the matrices and order of the matrix multiplications though.

Hi Arciera,

Nice work ! Impressive.

Hi Arciera,

Thank you for sharing your work with us. It's very impressive. And I have found it invaluable for setting up my own CNC machine.

I've worked through all the files except the remap.py file for the TWP functionality. Everything else seems to be working fine so far and I have a decent understanding of it all, but some help with the remap file would be much appreciated. I'm a little stuck on the opening section where it returns the A/B joint positions for a given tool-orientation vector. I don't fully understand the calculations and how they would need to be modified to suit my particular setup (A/B will become A/C).

As a bit of a background on my machine, I have a fixed table with a rotary B axis, and a moving gantry with an A,C head where the A axis is 55° nutating (similar to the Hiteco head shown here on page 1). I can provide more information if needed.

Basically I'm just looking for a bit of guidance for modifying the remap.py file other than the basics like updating the matrices and changing the values to match my kinematic model. Thanks again.

I didn't bother to type out that part of the documentation and my hand notes are long gone.
I'll see if I can retrace my steps but it may take me a few days to do so.

Ok, now it all came back to me:

To calculate the joint angles (which is done in the function 'kins_calc_jnt_angles' in 'remap.py' ) we use the rotation matrix part (ie disregard the fourth row with all the zeros ) of the transformation matrix as derived for the inverse tool kinematic:

 

the columns of this matrix represent the tool orientation vectors [tx, ty, tz] and hence the 3rd column represents the tool-z orientation vector we are trying to orient the spindle head to.
So using the variable names from the remap we get:

Kwx = Cb*t + Sb * u
Kwy = v
Kwz = -Sb*t + Cb*u

with the substitution for 'v' we can then solve for Sa and thus for the angle of joint A 
Then we use the two remaining equations to solve for Sb and thus for the angle of Joint B

The output of this calculation needs to conditioned so the correct angle values are output for the machine rotary joints.

As a side note:

in the function ' kins_calc_tool_rot_c_for_horizontal_x' of remap.py there is  this comment:

    # Mathematically we take the symbolic formula found in row 3, column 1 of the transformation
    # matrix from the inverse tool-kinematics, equal that to zero and solve for 'tc'.
    # ie: -(tctc-vstc)cb-(cactc-tstc)sb=0

  Note that the formula given in the comment may not be readily recognizable in the matrix shown above yet it is indeed identical to the third row of the first column. It seems that in the final version of the documentation 'Ctc' and 'Stc' were factored out instead of 'Cb' and 'Sb'.

 

Correction:
with the substitution for 'v' we can then solve for Sa and thus for the angle of joint A 

with the substitution for 'v' we can then solve for Ca and thus for the angle of joint A 

Thanks Aciera,

Your help means a lot. I wouldn't know how to do any of this on my own.

I've been trying to understand the if-else statements in 'remap.py' for the tool-orientation vector by substituting known values into the calculations, but my math is a little lacking so I still don't fully understand how the calculations work. And I presume I will need to change them if I have a 55° nutating head. For example, if Kwy = 1, A_j = pi and B_j = 0 will only work on a 45° nutating head.

The part of the calculations I understand the least are the parts of the if-else statements similar to this:

            if  -(sqrt(2)*Kwz*Sa_j) <= Sa_j*Sa_j:
                B_j = (- asin(2*(sqrt(2)*Kwz*Sa_j - (Ca_j + 1)*Kwx)/(Ca_j*Ca_j
                       + 2*Sa_j*Sa_j + 2*Ca_j + 1)))

A bit of an explanation about how this works would be great. I'll post the full section of code below.

The '-(tctc-vstc)cb-(cactc-tstc)sb=0' did confuse me for a second, but there was a note in the file stating it referred to row 3, column 1 of the inverse tool kinematic. It was easy enough to understand after this.