LinuxCNC S-Curve Accelerations

To bridge the gap until the developers have something. Many good servos already have this function. Example from the Delta manual

It seems to be veri good solution however no sure if this can be sincronized for at least 2 axis.

I was reading this interesting article about bezier curver
www.drdobbs.com/forward-difference-calcu...-of-bezier/184403417

and I think it can be helpfull to solve the maths

I've done some more work on this. I worked through the remaining equations and ended up with something I simply don't know how to solve. I believe it's a cubic equation, but it contains the root of a sum of the squared dependant and other variables:

t2^3 = 1/6*(6*a0^2*j0*t2 - 2*a0^3 + 6*j0^2*s_target - 6*(2*j0^2*t2 - a0*j0)*v0 - 3*(2*j0^2*t2^2 - a0^2 + 2*j0*v0)*sqrt(j0^2*t2^2 - 1/2*a0^2 + j0*v0))/j0^3, where t2 is the variable to solve for.

Anyway, I tired of banging my head against these equations, and decided to try a numerical solution for the remaining cases instead:
Of course a numerical (iterative) solution is not great in a real time system. I benchmarked the code - and got a bit of a shock when it reported ~100 ms for a solution! That's eons of computer time! Then I realised I had a lot of debug printouts. Rmoving them brought it down to ~7 ms. Still way too much. Maybe I should try an optimised build instead of a debug build? That gave another factor 10 improvement - but still too slow. Then I realised that maybe I don't need picometer accuracy *lol*. Changing it to 0.1 µm brought the calculation time down to less than 50 µs on my i5-3470 CPU. Still not great but at least it's in the realm of usability. For comparison, the cases where I have an analytical solution benchmarks at about 2-3 µs.

It should also be possible to optimise the algorithm to converge faster. And I haven't given up hope on an analytical solution, either. Maybe there's help to find at Mathematics Stack Exchange or even the local university, if needs be.

I still have a few test cases unaccounted for, but they should be variants of the ones I already have so should not present any huge difficulties. (One can hope, at least. ) Then it's off to integration with linuxcnc. One positive thing about using a numerical solution is that it doesn't need the cubic solver from the GNU Science Library, which removes the GPLv3 "taint".

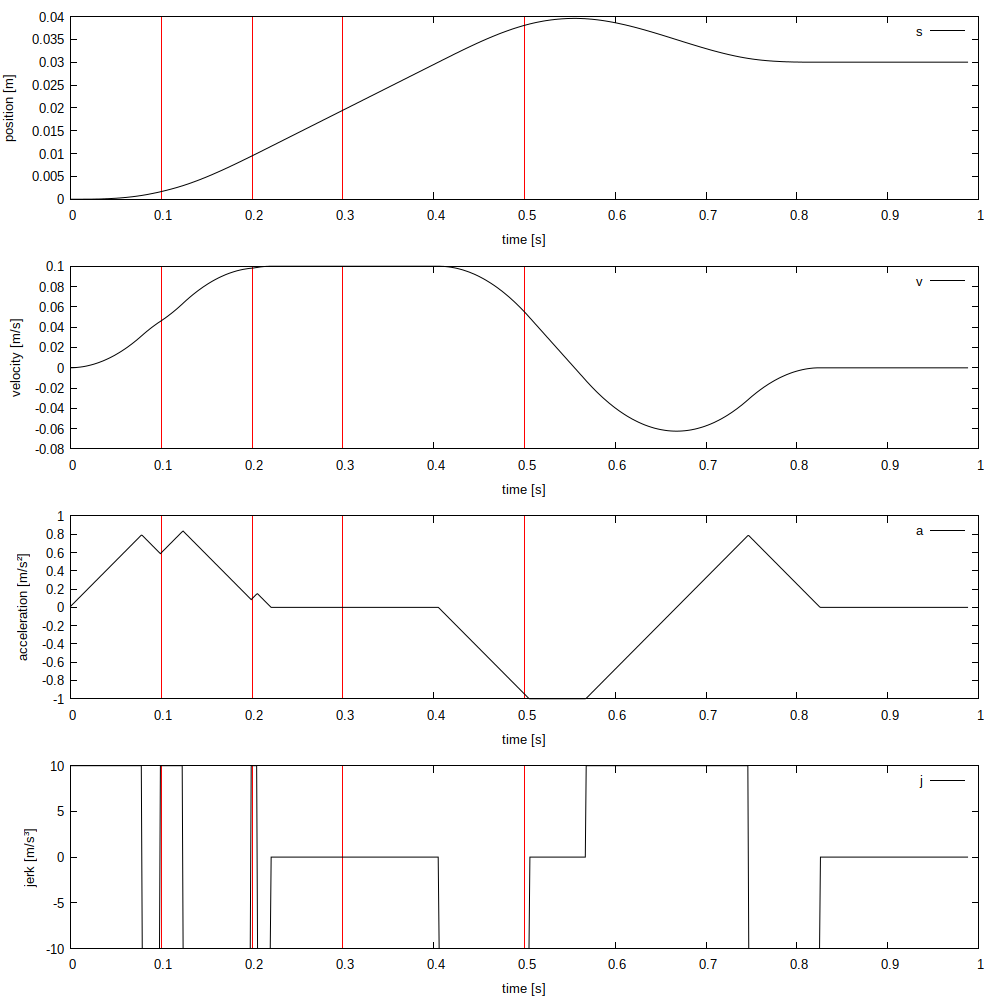
Here's the output of the "jlim_complex" test. It's supposed to model jogging with a (course) MPG. It sets the target position to 0.01 m at t = 0.0; 0.02 m at t = 0.1; 0.03 m at t = 0.2, 0.04 m at t = 0.3 and then back to 0.03 m at t = 0.5:

Ohh that one is easy to solve

I more wanted to point at a tool you might want to use.

Thanks, I already got pretty much the same thing out of Sage Math. I have no idea what to do with those sqrt(<something>*i) though!

Although those types of expressions do turn up when solving cubic expressions in general, so it's probably possible to do *something* useful with it!

Edit: After a closer look it looks like WolframAlpha did find a real solution - the j's are from the input equation? If so that equation could actually be useful.

Yes, as explained I had a solver for such equations from the GNU Science Library in the code, but the equation in question is not in the correct form, since it has roots of sums including the dependant variable in it. I'm not even entirely sure it is a cubic equation, but I'm guessing some math magic would turn it into one.

t2^3 = 1/6*(6*a0^2*j0*t2 - 2*a0^3 + 6*j0^2*s_target - 6*(2*j0^2*t2 - a0*j0)*v0 - 3*(2*j0^2*t2^2 - a0^2 + 2*j0*v0)*sqrt(j0^2*t2^2 - 1/2*a0^2 + j0*v0))/j0^3

Is the acceleration limit constant once LinuxCNC has started, or does it need to be modifiable on-the-run? If modifiable, is it applied immediately or only on new moves?

I'm working on integrating Smooth1d (my jerk-limited 1-axis planner) into LinuxCNC. Smooth1d has no need to remember the limits (velocity, acceleration and jerk) once a move has been planned. Simple_tp on the other hand keeps these as state, also between moves, and other parts of the code references this state. I'm trying to figure out if I should add this state to Smooth1d, just for convenience, or if it really belongs somewhere else.

Looking at motion.h there is a command EMCMOT_SET_JOINT_ACC_LIMIT. Is this used only to communicate the INI setting?

There is a field acc_limit in emcmot_joint_t, under the section "configuration info - changes rarely". Does this mean this value is in essense constant?

The only thing I've half observed is I think the acceleration is reduced when using MDI commands. I just never looked at it in detail v's the same move in gcode. It would be easy to confirm with halscope monitoring motion.current-vel for a straight line segment from the MDI and Gcode.

I think also becasue acceleration is per joint, where the segment is say at 45 degrees in the XY plane, the acceleration for the segment in the direction of the move may be above the joint limits (which are still respected).

Yeah, the reduced acceleration while jogging was discussed earlier in this thread: link .

What I'm after is if the acceleration value set in the INI file should be modifiable at a later time. Or is the value set in the INI a "machine constant"?

There are at least two arbitrary default values assigned to joint->acc_limit: in motion.c and in inijoint.cc . (They both happen to have the same value of 1.0.) Wouldn't it be better to require a setting for these obligatory limits and refuse to start if they are missing? This way there would be no risk of starting with essentially random settings, and the machine wouldn't behave differently depending on the machine units chosen.

Would it be possible to specify constant settings to motmod.so on load, as parameters, instead of via EMCMOT commands? I'm still a bit hazy on how the loading of the different modules work...