Trajectory Planner using Ruckig Lib

Arc to arc tri-clothoid g2 solving works. Tested line to arc, works ok.

This is more difficult to code. As we need the arc angle at the tip of the arc circumfence.

For the first arc endpoint:
1. We first find the angle of the line pc to p1. (pc = center, p1=arc endpoint). This is atan angle to x-axis.
2. We calculate if arc is cw or ccw. (cw=clockwise, ccw=counterclockwise).
3. We add +90 or -90 degrees to the angle calculated by 1, depends on cw or ccw direction. This is then the tip angle of the arc.

For the second arc startpoint:
1. angle pc to p0.
2. calculate direction cw or ccw.
3. We add +90 or -90 degrees to angle found at 1. But then this is opposite input of first arc, i found out.

Sample picture of the fillet :
 

Video, mention it only draw's an arc when it's not a line.

 

Hi,

We now have opencascade ready to draw the clothoid fillets. opencascade functions
It automaticly knows if the first & second item is a line or arc.
Then it does some logic and connects them with tri-clothoid.

Now tommorow i will make a clothoid list. This are interconnected clothoids that can be a gcode overlay path.
This result is then a gcode path with G2 continuity. The G2 problem is then solved.

We will see what the result may be. I am quite qurious. The code now does not involve path deviation value, as
this can be done when gcode path overlay works.
Also i can look at the gcode compressor to filter out tiny segments.

The clothoid can be a line, an arc or a spline. Its like a thing that can change.

 Ok have a nice day !
 

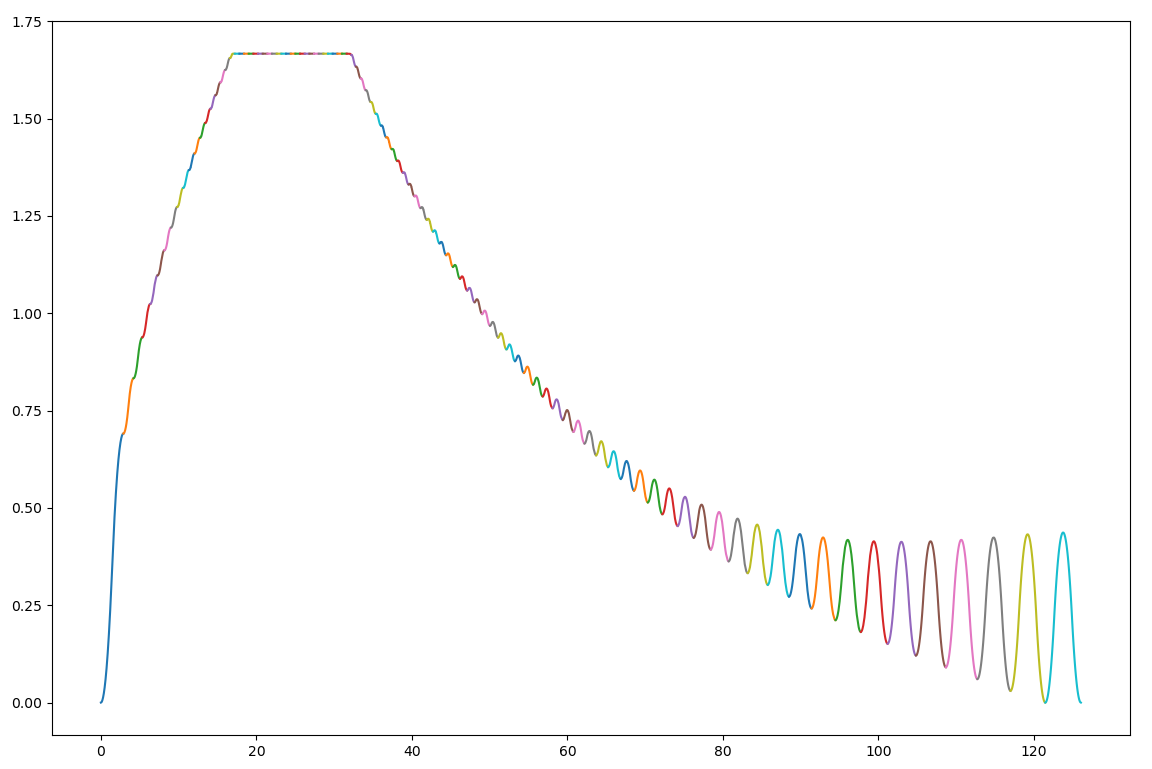
The s-curve multi-segment solver is working efficiently now. This is 100 1.0in segments with a v_max of 100in/min, a_max of 40in/min, and j_max of 20in/min. The oscillations on the second half of the path are because I'm using a very crude method of solving velocity overshoot from the end of one segment to the start of the next segment. I need to figure out another set of equations to get the second half to look nice like the first half.



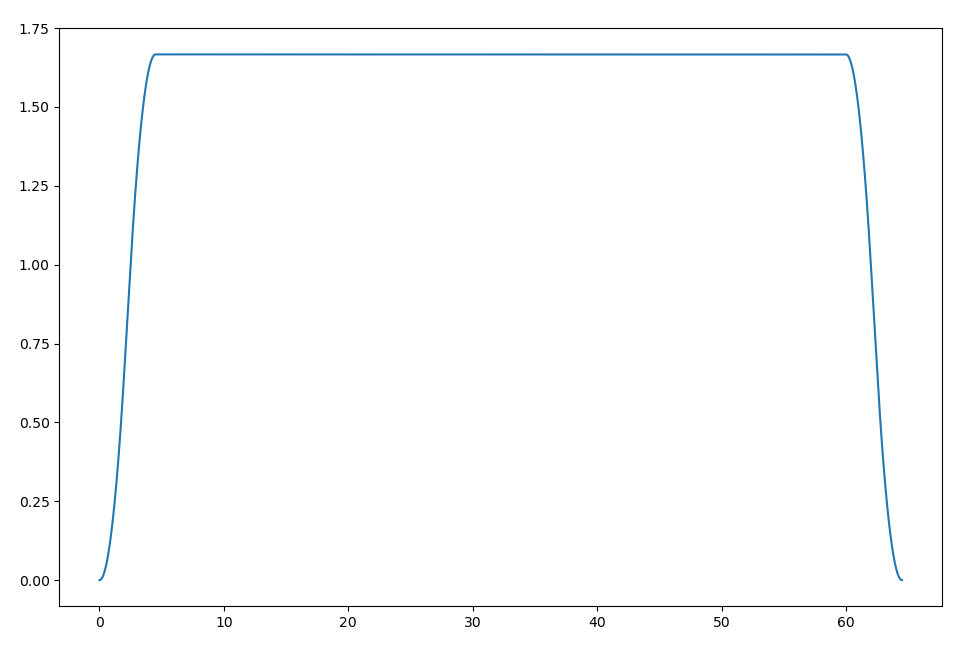
You can see how this contrasts with a single 100in segment with the same constraints. This is because each s-curve has to begin and end with zero acceleration.


Edit: This is better, but not super efficient.

@Andrew,

Are u using acceleration begin and or acceleration end values within your code?
Then you could start somewhere on the curve and finish where you want.

@All,

After a long day of cleaning up old code, i have made a video off the current situation related to tri-clothoid fillets.
Here we solve the G2 problem in 3d. Hold on. It's like magic.



The blue is the 2d projection where the actual clothoid 2d calculation happens. You cant see it, but its done over there.
Then after this, the projection is transformed back into the current plane.
This works for all combinations line, arc.




 

There is a maximum acceleration and maximum deceleration, but the start and end acceleration of each s-curve is zero. It would be nice if the initial and final acceleration could be chosen, but I think that would be computationally infeasible to do in near real-time. Of all of the papers I've looked at, none had a solution where you could have an initial and final acceleration constraint.

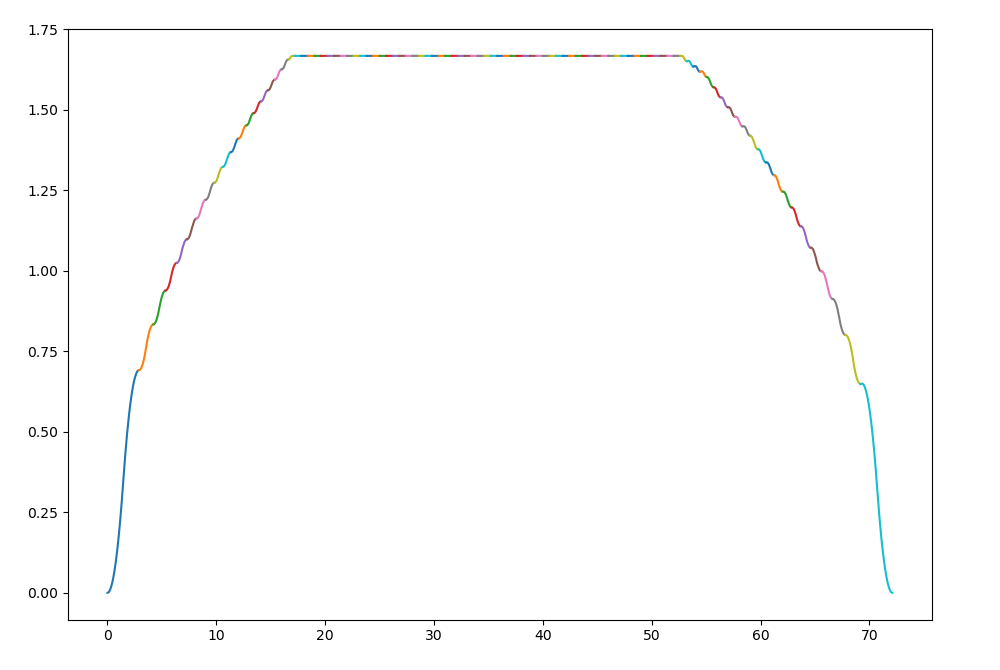
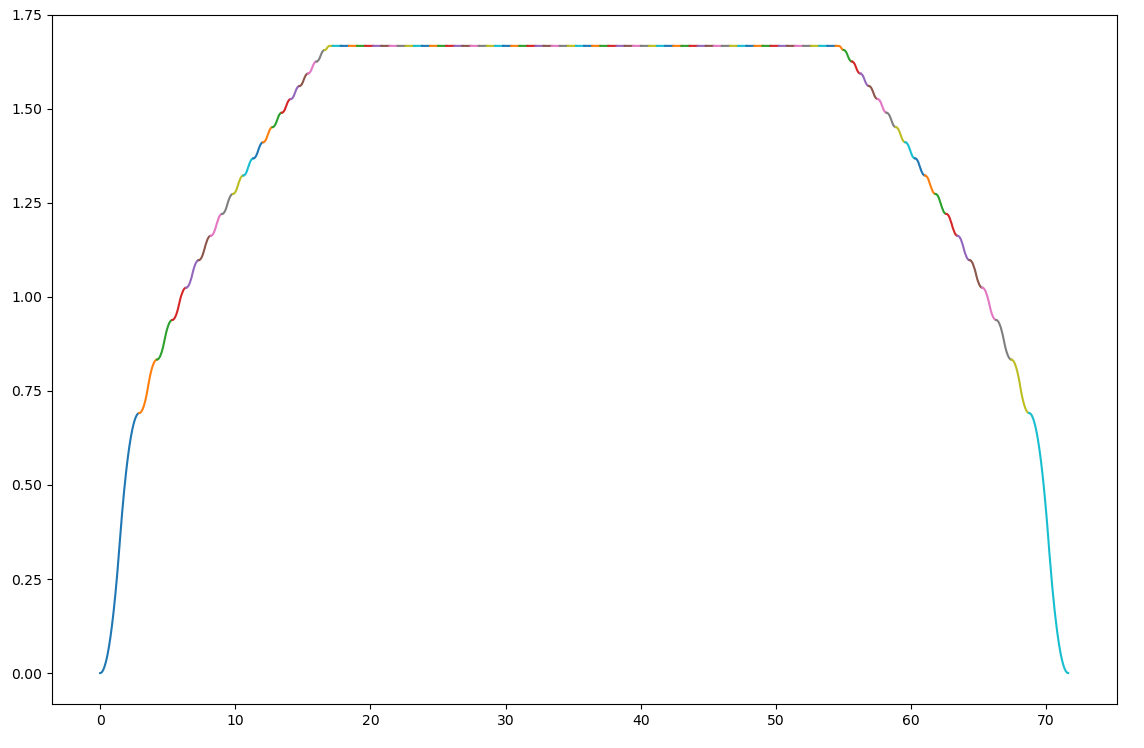
I got it working. All the algorithms needed to solve the problem efficiently have been figured out. At this point it's just about cleaning up code and dealing with any bugs that pop up. This takes about 500us to solve 100 s-curve segments with velocity and acceleration continuity and no work has been done to try to optimize anything yet.
 

There is a maximum acceleration and maximum deceleration, but the start and end acceleration of each s-curve is zero. It would be nice if the initial and final acceleration could be chosen, but I think that would be computationally infeasible to do in near real-time. Of all of the papers I've looked at, none had a solution where you could have a initial and final acceleration constraint.

In the papers, maybe they say nothing about acceleration begin, end values.
But there is a trick to use it. You just have to use a workaround.

Link : example

Isn't this the code for jogging? The s-curve solver I'm working on is for planning, where the final velocity and distance are known ahead of time and the seven segment time periods need to be solved. I don't think that would work for this. Currently, to get a solution, quadratic, cubic, and quartic polynomial roots need to be solved for. I'm pretty sure if an initial and final acceleration constraint were added it would turn into a problem with no closed-form solutions and need to be solved by some type of iterative algorithm which would be much slower and more complex.

The acceleration here is just linear acceleration. You can still use this even in the middle of a curve. The constraints you would need to set are the max jerk, max acceleration, and max velocity. The velocity on the curve would determine the centripetal acceleration and jerk, and the total jerk and acceleration would be those plus the linear acceleration and jerk where all of them are vectors.

@Andrew,
Isn't this the code for jogging?

It's for both jogging & auto mode (planning).
There is a demo program written in qt that shows auto mode & jog mode.

I am curious to your solution.

Yes, I'm also super curious how yours works in planning mode. If you give yours the same problem to solve, what does the graph look like compared to mine? The problem in my graph is 100 segments of:

// units of inches and seconds, so 100in/min etc
V = 100.0/60; // max velocity
A = 40.0/60; // max acceleration
D = 40.0/60; // max deceleration
J = 20.0/60; // max jerk
L = 1.0; // distance

The initial velocity of the first segment is constrained to 0, and the final velocity of the last segment is constrained to 0. Since there are one-hundred 1in segments, the total distance traveled should be 100in.

hi Grotius.
Listen, I wanted to consult with you about the trajectory planner. As I understand, you chose a G-code-based planner for LinuxCNC. I have already figured out the Ruckig library and made a fully functional utility that works with an EtherCAT motor. Now, I want to find a convenient trajectory planner. I initially chose MoveIt2 because it is recommended on the Ruckig page. However, it seems to be overly complicated, and I've been trying to set it up with GPT chat for a day now. Additionally, ROS2 needs to be installed, and so on. In general, do you have any recommendations for a planner? There's also the option of Tesseract, but maybe there is something more convenient?
best regard