scurve trajectory planner

@Bkt,

Did you do a vision system study?
Greetings.

Hi,

Here is the first test result of the triangle centroid path smooth algo.
The algo is not finished yet, as this is only the first iteration. The second
iteration smooth's even more.

G64 P5 => it indeed filters out the 5mm spikes in the gcode.

Scurve + cenroid smooth
 

Original planner
 

Hi,

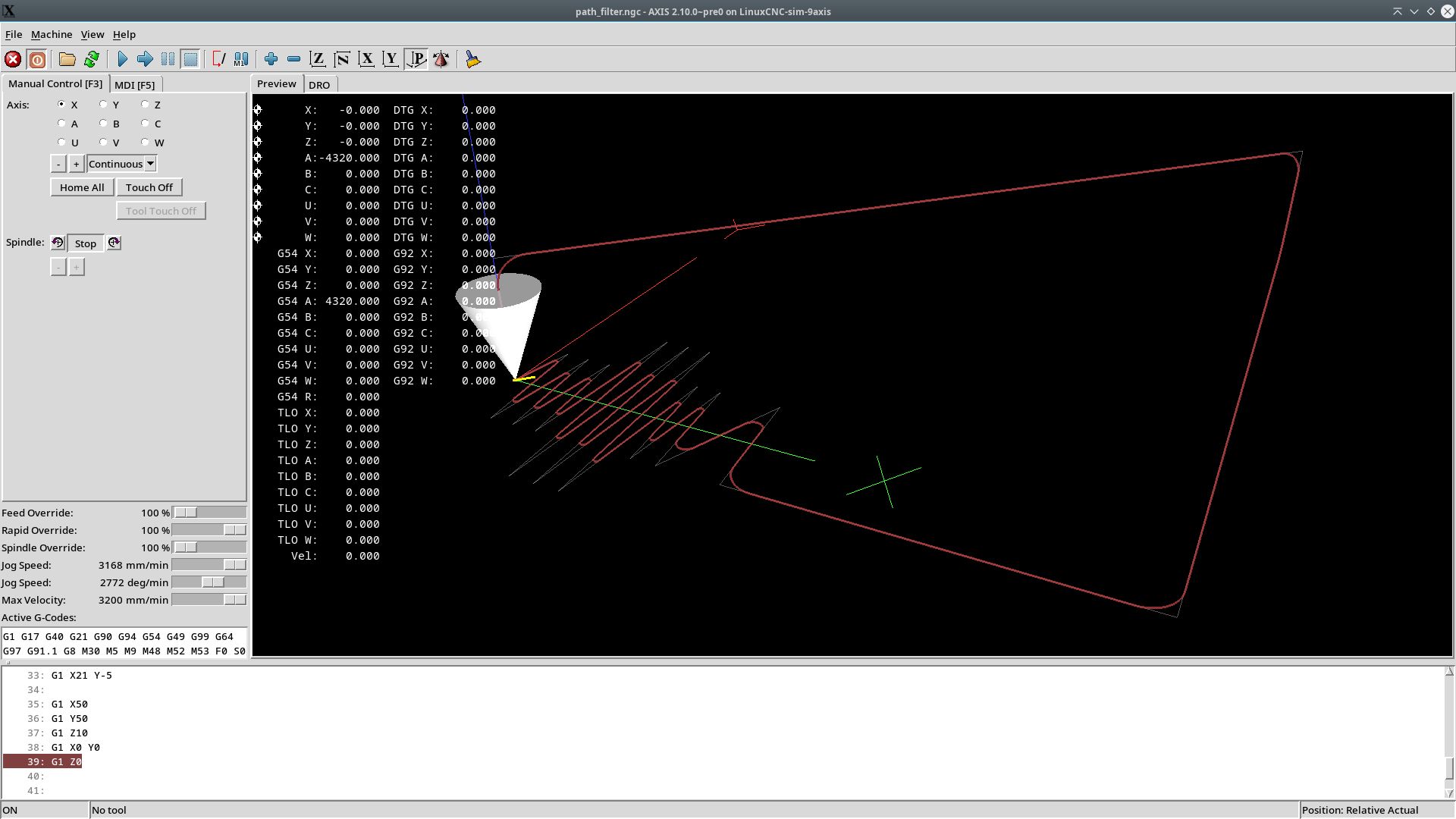
I changed the planner's infrastructure so it can use different smooth algo's easy.
This was quite a lot off work.

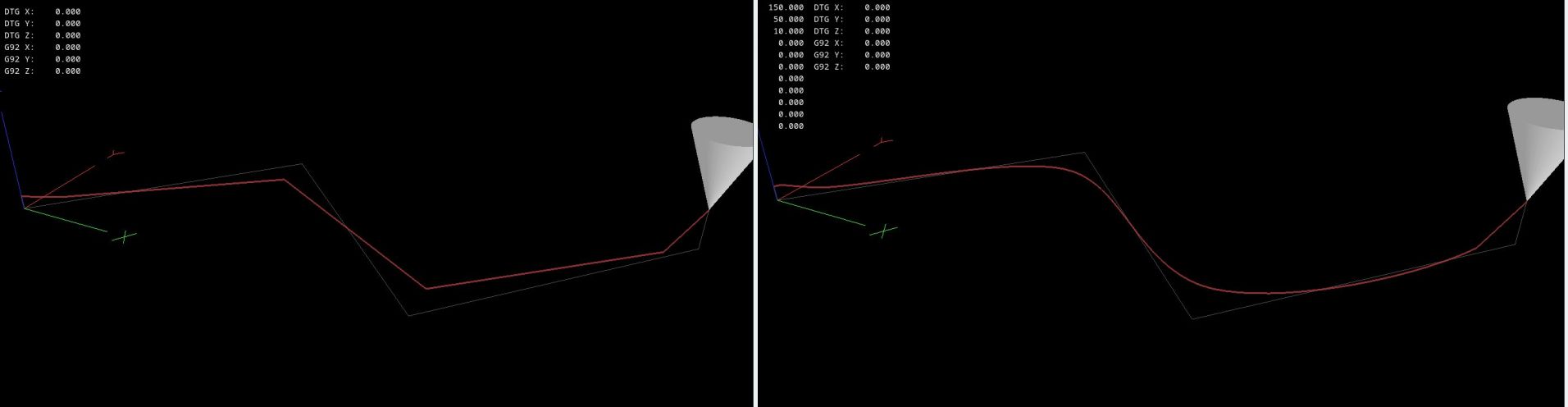
Now this is the centroid smooth algo on the left. First iteration.
And a catmull rom spline on the right. Second iteration.
The distance from the corners to the spline is the exact G64 P[x] value.
First and last gcode line are original, not curved.

oooh

I build a small pyvcp side panel and did some gcode coding to build a test program. Not finished yet, but I think it will be handy for testing.

Random values and one can change the limits on the go via the panel.

Sorry for the bad video and picture quality. 
Video

@Julian,

Thanks for creating a test configuration. This is really helpfull.

I’ve been dealing with an issue related to acceleration spikes in the HAL scope output for joint.0-acc-cmd and joint.1-acc-cmd during runtime, specifically when interpolating splines. I wanted to share the problem, its root cause, and the solution I’ve implemented in case it helps others facing similar challenges.

The Problem:
When interpolating lines or arcs, the HAL scope output for joint.0-acc and joint.0-acc behaves as expected. However, when interpolating splines, I observe acceleration spikes in the HAL scope. These spikes are problematic and can lead to undesirable behavior in the motion system.

Root cause:
The issue arises from how splines are interpolated. Splines are typically interpolated based on their total length, which is calculated by evaluating a finite number of points (e.g., 20 points) along the spline trajectory. Unlike lines or arcs, the absolute length of a spline cannot be calculated mathematically in a straightforward manner. This also applies to more exotic curves.When the spline is treated as a series of connected line segments (a "linestrip"), each segment has an angle relative to the next. These angular changes cause abrupt direction changes during interpolation, resulting in acceleration spikes. The same issue occurs if the spline length is pre-calculated and interpolated from t=0 to t=1 acceleration spikes still appear in the output.

Possible solutions:

1. Filtering Acceleration Spikes:
   One approach is to filter out the acceleration spikes by using a stepgen backend for XYZ joints. However, this is more of a workaround than a true solution.
2. Restricting Curve Types:
   Another option is to use only curves whose lengths can be calculated absolutely (e.g., lines and arcs). While this avoids the problem, it limits the flexibility of the system.

My Solution: Arc-Strip Interpolation
After much thought, I designed a solution that allows the use of any smooth algorithm or exotic curve without introducing acceleration spikes. Here’s how it works:

1. Waypoint Generation:
   The curve is transformed into a fixed number of waypoints (e.g., 21 waypoints). The number of waypoints can be adjusted (e.g., 9 or 51) depending on the desired precision.
2. Arc-Strip Interpolation:
   At runtime, an arc-strip interpolator processes these waypoints. The interpolator treats the curve as a series of connected arcs rather than lines. For example, 21 waypoints can be divided into 7 arcs (since each arc requires 3 waypoints). The total length of these arcs is known absolutely, eliminating the need for approximate length calculations.
    

By treating the curve as a series of arcs (an "arc-strip"), the system avoids the abrupt direction changes that cause acceleration spikes. This approach maintains smooth motion and works well for a wide variety of curves.

Why This Works:

• Smooth Transitions: Arcs inherently provide smoother transitions between points compared to straight lines, reducing abrupt changes in direction.
• Absolute Length Calculation: The total length of the arc-strip is known precisely, avoiding the approximation errors associated with spline length calculations.
• Flexibility: This method can be applied to any curve type, including exotic curves, as long as it can be represented by a series of waypoints.
   

Conclusion:
This solution has resolved the acceleration spike issue in my system and allows for the use of complex curves without compromising motion quality. I hope this explanation and approach can help others facing similar challenges. If anyone has further insights or alternative solutions, I’d love to hear them! 

The implementation of an exotic curve into the planner.

1. Curve absolute length is known.
2. Minimal direction changes during curve interpolation at runtime.

 

Hi Grotius,
I sent you an email last month about the servo and stepper drives. Hope you have received it.

I am also seeing the same acceleration peaks in the joint command acceleration.

Inhave a suggestion: clothoid length can be calculated easily by knowing the start and end curvature radius and the clothoid parameter A.

www.geogebra.org/m/pPu6Kb3z#:~:text=Clot...20A2%20is%20constant.

math.stackexchange.com/questions/3287710...-of-clothoid-segment

Maybe clothoida are the way to go for 3 axis geometries. Beyond that I am having a hard time imagining what a clothoid would look like in higher dimensions.

-automata

Keep up the good work guys!
There might be obstacles but there is light at the end of the tunnel!