scurve trajectory planner
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-

Less
More
- Posts: 2419
- Thank you received: 2343
29 Mar 2025 12:51 #325243
by Grotius
Replied by Grotius on topic scurve trajectory planner
Please Log in or Create an account to join the conversation.
- FabianB
-

- Offline
- New Member
-

Less
More
- Posts: 14
- Thank you received: 19
01 Apr 2025 13:10 #325463
by FabianB
Replied by FabianB on topic linuxcnc scurve motion planner
Hi Grothus,
always impressive how fast you make progress here.
Did you have a closer look at the problem you called "overfitting"? It looks not like classical overfitting (this usually descibes if a fit follows the data much to closely and therefore follows statiscal fluctuations instead of the desired data trend).
In your case it just found a local minimum during fitting instead of the global minimum. Doing a 360 or creating this sort of step in the corner is a viable solution that is quite smooth etc. it is just not the solution we want.
One possibillity to avoid this would be to somehow create a better initial guess before the fitting starts. This could also reduce the iterations/time needed for fitting. Another possibillity might be to use a different solver.
Best regards,
Fabian
always impressive how fast you make progress here.
Did you have a closer look at the problem you called "overfitting"? It looks not like classical overfitting (this usually descibes if a fit follows the data much to closely and therefore follows statiscal fluctuations instead of the desired data trend).
In your case it just found a local minimum during fitting instead of the global minimum. Doing a 360 or creating this sort of step in the corner is a viable solution that is quite smooth etc. it is just not the solution we want.
One possibillity to avoid this would be to somehow create a better initial guess before the fitting starts. This could also reduce the iterations/time needed for fitting. Another possibillity might be to use a different solver.
Best regards,
Fabian
The following user(s) said Thank You: Grotius, DauntlessA
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-

Less
More
- Posts: 2419
- Thank you received: 2343
01 Apr 2025 15:21 #325468
by Grotius
Replied by Grotius on topic linuxcnc scurve motion planner
Hi Fabian.
In the mean time i experimented with clothoid used for motion. This includes 2 attached clothoids for example.
Now the problem is not the ceres solver, the iterations, or the initial guess value. All these are ok.
It takes about ~12 iterations to fit the clothoid.
There are certain gcode files that have very short segment attached to longer segments under 90 degree angle.
Then the trim algo trims both segments given the P value. But the very short segment is trimmed less then the longer segment.
The clothoid result is valid, however it path can be into the workpiece.
Soon i will show a picture how this looks like. I think the solution lies in even trimming to both segments in some cases, or in all cases.
The solution is therefore quite simple.
In the mean time i experimented with clothoid used for motion. This includes 2 attached clothoids for example.
Now the problem is not the ceres solver, the iterations, or the initial guess value. All these are ok.
It takes about ~12 iterations to fit the clothoid.
There are certain gcode files that have very short segment attached to longer segments under 90 degree angle.
Then the trim algo trims both segments given the P value. But the very short segment is trimmed less then the longer segment.
The clothoid result is valid, however it path can be into the workpiece.
Soon i will show a picture how this looks like. I think the solution lies in even trimming to both segments in some cases, or in all cases.
The solution is therefore quite simple.
The following user(s) said Thank You: DauntlessA
Please Log in or Create an account to join the conversation.
- DauntlessA
- Offline
- Junior Member
-

Less
More
- Posts: 23
- Thank you received: 5
01 Apr 2025 16:40 #325470
by DauntlessA
Replied by DauntlessA on topic linuxcnc scurve motion planner
Fabian,
Yes, I agree that overfitting doesn't exactly describe what is happening.
I was meaning to post some additional info I found on this. It's one of Raph Levien's blog post on fitting cubic Bézier curves, (specifically in the section on the solutions for quartic polynominals):
raphlinus.github.io/curves/2021/03/11/bezier-fitting.html
My understanding is that in his case, the degree of the curve (in this example quartic) and the fact that there are two parameters (x-moment and signed area) leads to four minimal solutions that the solver could converge to (not infinite solutions, luckily!). I believe that in Raph's case, three of these will be local minima and only one will be the global minimum, so we cannot be certain of converging to the global minimum if we start at a random position in the parameter space, as you said.
Raph says that one of these solutions (when optimising for x-moment and signed area) may contain a loop. This is a valid solution to these parameters because the area inside the loop has the opposite sign to the outside, so the signed area is still minimised.
Raph says that you can generally reject this solution as the arm length is longer than the others. But my understanding is that you can only do this by calculating multiple solutions and rejecting the one with the extreme arm length. You can only do this if you obtain at least two solutions, and even then both may have issues.
What might be happening is that you're regularly converging to a non-global minimum, but normally it's so similar to the global minimum that it isn't evident in the result. It's only when you converge to the solution with the extreme arm length that you notice an issue.
Grotius,
I think your method of fixing this by applying a tiny offset worked because it meant that the the loop was no longer complete so its signed area was a lot larger. Although likewise, adding this offset could technically break a curve which would have worked without it? But that's most likely an edge case.
Also, slightly off-topic, but there might also be instances where this loop with the extreme arm length is the solution the user intended. For example, the intended path did have this loop, but under-sampling in the CAM software means that points are missing which should explicitly indicate the presence of the loop. But since this information is missing, it's probably better to treat this as a bug, and reaffirm that the trajectory planner may choose a solution which doesn't match the path you intended. The way to get around this is to increase your sampling frequency in your CAM software.
Back on topic, the way I see it is that the most rigorous way to solve this problem is to start from enough locations in the parameter space that you obtain all (or some) of the local minima, meaning you can be certain of having found the global minimum (or be sure enough of being close to it). But this is computationally expensive and harder to predict how long it will take to return its output.
So it's probably better to find shortcuts which make you more certain that if you converge to a single value, it's good enough even if not the global minimum. I think the idea you mentioned of initially fitting lower-order curves should help with this.
It also seems that using the gradient descent method along with the appropriate number of parameters will increase this probability of you finding the global minimum.
But I understand that some of these solutions are antagonistic to making the solver work fast, even if it is in a separate thread.
Yes, I agree that overfitting doesn't exactly describe what is happening.
I was meaning to post some additional info I found on this. It's one of Raph Levien's blog post on fitting cubic Bézier curves, (specifically in the section on the solutions for quartic polynominals):
raphlinus.github.io/curves/2021/03/11/bezier-fitting.html
My understanding is that in his case, the degree of the curve (in this example quartic) and the fact that there are two parameters (x-moment and signed area) leads to four minimal solutions that the solver could converge to (not infinite solutions, luckily!). I believe that in Raph's case, three of these will be local minima and only one will be the global minimum, so we cannot be certain of converging to the global minimum if we start at a random position in the parameter space, as you said.
Raph says that one of these solutions (when optimising for x-moment and signed area) may contain a loop. This is a valid solution to these parameters because the area inside the loop has the opposite sign to the outside, so the signed area is still minimised.
Raph says that you can generally reject this solution as the arm length is longer than the others. But my understanding is that you can only do this by calculating multiple solutions and rejecting the one with the extreme arm length. You can only do this if you obtain at least two solutions, and even then both may have issues.
What might be happening is that you're regularly converging to a non-global minimum, but normally it's so similar to the global minimum that it isn't evident in the result. It's only when you converge to the solution with the extreme arm length that you notice an issue.
Grotius,
I think your method of fixing this by applying a tiny offset worked because it meant that the the loop was no longer complete so its signed area was a lot larger. Although likewise, adding this offset could technically break a curve which would have worked without it? But that's most likely an edge case.
Also, slightly off-topic, but there might also be instances where this loop with the extreme arm length is the solution the user intended. For example, the intended path did have this loop, but under-sampling in the CAM software means that points are missing which should explicitly indicate the presence of the loop. But since this information is missing, it's probably better to treat this as a bug, and reaffirm that the trajectory planner may choose a solution which doesn't match the path you intended. The way to get around this is to increase your sampling frequency in your CAM software.
Back on topic, the way I see it is that the most rigorous way to solve this problem is to start from enough locations in the parameter space that you obtain all (or some) of the local minima, meaning you can be certain of having found the global minimum (or be sure enough of being close to it). But this is computationally expensive and harder to predict how long it will take to return its output.
So it's probably better to find shortcuts which make you more certain that if you converge to a single value, it's good enough even if not the global minimum. I think the idea you mentioned of initially fitting lower-order curves should help with this.
It also seems that using the gradient descent method along with the appropriate number of parameters will increase this probability of you finding the global minimum.
But I understand that some of these solutions are antagonistic to making the solver work fast, even if it is in a separate thread.
The following user(s) said Thank You: Grotius
Please Log in or Create an account to join the conversation.
- FabianB
-

- Offline
- New Member
-

Less
More
- Posts: 14
- Thank you received: 19
02 Apr 2025 09:20 - 02 Apr 2025 09:31 #325503
by FabianB
Replied by FabianB on topic linuxcnc scurve motion planner
I also think that finding all solutions and picking the best might be quite complicated and also computationally expensive. I hope starting with a slightly better initial guess that's closer to the desired global minimum will get us there already.
@Grotius what are currently the starting values for the fit? I assume the boundary conditions from the two endpoints for curvature and torsion. Maybe we can find a good set of vlues for the other parameters. Maybe something that is close to a simple arc connecting the points or something similar.
@Grotius what are currently the starting values for the fit? I assume the boundary conditions from the two endpoints for curvature and torsion. Maybe we can find a good set of vlues for the other parameters. Maybe something that is close to a simple arc connecting the points or something similar.
Last edit: 02 Apr 2025 09:31 by FabianB.
The following user(s) said Thank You: DauntlessA
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4531
- Thank you received: 2015
02 Apr 2025 11:34 - 02 Apr 2025 11:51 #325510
by Aciera
Replied by Aciera on topic linuxcnc scurve motion planner
Just to recap:
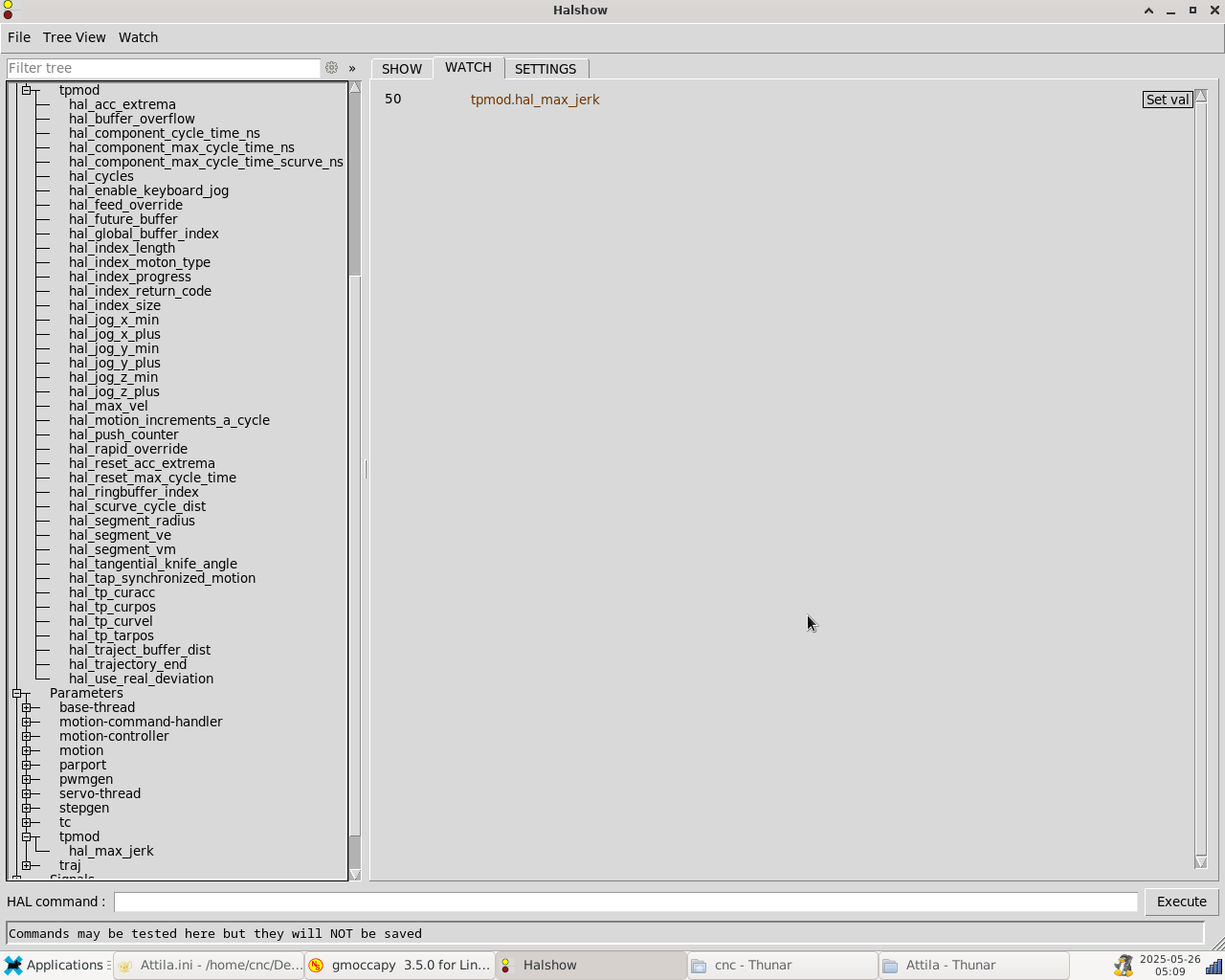
The solver uses variables gamma_1, gamma_2 and s_1 to minimize the distance between the end point of the 4th clothoid segment and the start of the trimmed back 2nd corner segment.
's_1' is the arc length of a clothoid segment (all four segments being of the same length).
'gamma_1', 'gamma_2' are parameters used for 3d clothoids and are both zero for a 2d clothoid
The starting values are here, if I'm not mistaken:
The solver uses variables gamma_1, gamma_2 and s_1 to minimize the distance between the end point of the 4th clothoid segment and the start of the trimmed back 2nd corner segment.
's_1' is the arc length of a clothoid segment (all four segments being of the same length).
'gamma_1', 'gamma_2' are parameters used for 3d clothoids and are both zero for a 2d clothoid
The starting values are here, if I'm not mistaken:
Attachments:
Last edit: 02 Apr 2025 11:51 by Aciera.
The following user(s) said Thank You: akb1212, Grotius, DauntlessA
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-

Less
More
- Posts: 2419
- Thank you received: 2343
02 Apr 2025 23:28 #325559
by Grotius
Replied by Grotius on topic linuxcnc scurve motion planner
@DauntlessA
I think your method of fixing this by applying a tiny offset worked because it meant that the the loop was no longer complete so its signed area was a lot larger. Although likewise, adding this offset could technically break a curve which would have worked without it?
The offset is not breaking the curve, and the curve is valid without this offset.
The 1e-12 offset was made to get the curve out off a singularity.
The 4-clothoid constrain formula has this result in rare cases where local clothoid plane alignes with global world plane.
We have input xy angle, input z angle for the clothoid fit.
The abstract could also use vector rotation as input, wich can be used to set the
torsion in and out rotations. Technically you can create clothoid helixes using this torsion turn value. But the abstract does not
use this oppertunity.
@Arciera,
Thanks for your contribution!
I think your method of fixing this by applying a tiny offset worked because it meant that the the loop was no longer complete so its signed area was a lot larger. Although likewise, adding this offset could technically break a curve which would have worked without it?
The offset is not breaking the curve, and the curve is valid without this offset.
The 1e-12 offset was made to get the curve out off a singularity.
The 4-clothoid constrain formula has this result in rare cases where local clothoid plane alignes with global world plane.
We have input xy angle, input z angle for the clothoid fit.
The abstract could also use vector rotation as input, wich can be used to set the
torsion in and out rotations. Technically you can create clothoid helixes using this torsion turn value. But the abstract does not
use this oppertunity.
@Arciera,
Thanks for your contribution!
The following user(s) said Thank You: akb1212, HalaszAttila, DauntlessA
Please Log in or Create an account to join the conversation.
- HalaszAttila
- Offline
- Premium Member
-
Less
More
- Posts: 149
- Thank you received: 5
23 May 2025 12:06 #328973
by HalaszAttila
Replied by HalaszAttila on topic scurve trajectory planner
Hello,
I tested the S-curve feature on the following system:
PC: HP with Intel i3 3rd Gen, 2x4GB RAM (latency < 20k)
OS: Debian 12
LinuxCNC: 2.10 pre-release
I created an XYZ mill configuration using StepConf and ran the same G-code with and without tpmod_scurve.
The results can be seen in the attached videos.
Observations:
Without the S-curve, the feed rate remains continuous.
With the S-curve enabled, the feed fluctuates significantly—at times dropping to 1/10 of the programmed feed rate.
It also noticeably increases the overall program execution time (2,5x slower with scurve in this situation).
I tried increasing VECTOR_BUFFER_SIZE to 100, but it didn’t help much. (Just for testing, I also set VECTOR_BUFFER_SIZE = 2, which made the behavior even worse.)
Maximum velocity and acceleration settings are visible in the video (they’re not particularly high, and are the same in both cases).
Question:
Do you think it's possible to achieve a continuous feed rate using the S-curve?
Files:
drive.google.com/drive/folders/1uR1LfCv_...4-w6Daf8?usp=sharing
I tested the S-curve feature on the following system:
PC: HP with Intel i3 3rd Gen, 2x4GB RAM (latency < 20k)
OS: Debian 12
LinuxCNC: 2.10 pre-release
I created an XYZ mill configuration using StepConf and ran the same G-code with and without tpmod_scurve.
The results can be seen in the attached videos.
Observations:
Without the S-curve, the feed rate remains continuous.
With the S-curve enabled, the feed fluctuates significantly—at times dropping to 1/10 of the programmed feed rate.
It also noticeably increases the overall program execution time (2,5x slower with scurve in this situation).
I tried increasing VECTOR_BUFFER_SIZE to 100, but it didn’t help much. (Just for testing, I also set VECTOR_BUFFER_SIZE = 2, which made the behavior even worse.)
Maximum velocity and acceleration settings are visible in the video (they’re not particularly high, and are the same in both cases).
Question:
Do you think it's possible to achieve a continuous feed rate using the S-curve?
Files:
drive.google.com/drive/folders/1uR1LfCv_...4-w6Daf8?usp=sharing
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-

Less
More
- Posts: 2419
- Thank you received: 2343
25 May 2025 11:57 #329104
by Grotius
Replied by Grotius on topic scurve trajectory planner
Hi Halas,
There is added a hal param for inertia wich can be set to from 0 up to 1 to run at programmed feed.
This results in less feed fluctiations at corners.
See the param section : readme.
Also program execution time should be faster. As i reverted the acc max change.
There is added a hal param for inertia wich can be set to from 0 up to 1 to run at programmed feed.
This results in less feed fluctiations at corners.
See the param section : readme.
Also program execution time should be faster. As i reverted the acc max change.
The following user(s) said Thank You: HalaszAttila
Please Log in or Create an account to join the conversation.
- HalaszAttila
- Offline
- Premium Member
-
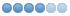
Less
More
- Posts: 149
- Thank you received: 5
26 May 2025 11:48 #329153
by HalaszAttila
Replied by HalaszAttila on topic scurve trajectory planner
Do you mean the hal_inertia_factor parameter?
Sorry, but I can't find this parameter (neither in halshow nor in the source code).
"Also, the program execution time should be faster."
Are you suggesting lowering this value: SERVO_PERIOD = 1000000,
or this one:
[TASK]
TASK = milltask
CYCLE_TIME = 0.001
I performed the above-mentioned tests with these settings.
Sorry, but I can't find this parameter (neither in halshow nor in the source code).
"Also, the program execution time should be faster."
Are you suggesting lowering this value: SERVO_PERIOD = 1000000,
or this one:
[TASK]
TASK = milltask
CYCLE_TIME = 0.001
I performed the above-mentioned tests with these settings.
Attachments:
Please Log in or Create an account to join the conversation.
Time to create page: 0.160 seconds