scurve trajectory planner
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
20 Feb 2025 15:21 - 20 Feb 2025 15:23 #322077
by Aciera
Replied by Aciera on topic scurve trajectory planner
This is what I'm working with (compiles and runs without the 'fdf.fvv' function which I don't know anything about while I could probably figure out the fdf.df Jacobian ):
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_multifit_nlinear.h>
/* parameters to model */
struct model_params
{
double a1;
double a2;
double a3;
double a4;
double a5;
};
/* Branin function */
int
func_f (const gsl_vector * x, void *params, gsl_vector * f)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double x2 = gsl_vector_get(x, 1);
double f1 = x2 + par->a1 * x1 * x1 + par->a2 * x1 + par->a3;
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * cos(x1));
gsl_vector_set(f, 0, f1);
gsl_vector_set(f, 1, f2);
return GSL_SUCCESS;
}
int
func_df (const gsl_vector * x, void *params, gsl_matrix * J)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * cos(x1));
gsl_matrix_set(J, 0, 0, 2.0 * par->a1 * x1 + par->a2);
gsl_matrix_set(J, 0, 1, 1.0);
gsl_matrix_set(J, 1, 0, -0.5 * par->a4 / f2 * (1.0 - par->a5) * sin(x1));
gsl_matrix_set(J, 1, 1, 0.0);
return GSL_SUCCESS;
}
int
func_fvv (const gsl_vector * x, const gsl_vector * v,
void *params, gsl_vector * fvv)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double v1 = gsl_vector_get(v, 0);
double c = cos(x1);
double s = sin(x1);
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * c);
double t = 0.5 * par->a4 * (1.0 - par->a5) / f2;
gsl_vector_set(fvv, 0, 2.0 * par->a1 * v1 * v1);
gsl_vector_set(fvv, 1, -t * (c + s*s/f2) * v1 * v1);
return GSL_SUCCESS;
}
void
callback(const size_t iter, void *params,
const gsl_multifit_nlinear_workspace *w)
{
gsl_vector * x = gsl_multifit_nlinear_position(w);
double x1 = gsl_vector_get(x, 0);
double x2 = gsl_vector_get(x, 1);
/* print out current location */
printf("%f %f\n", x1, x2);
}
void
solve_system(gsl_vector *x0, gsl_multifit_nlinear_fdf *fdf,
gsl_multifit_nlinear_parameters *params)
{
const gsl_multifit_nlinear_type *T = gsl_multifit_nlinear_trust;
const size_t max_iter = 200;
const double xtol = 1.0e-8;
const double gtol = 1.0e-8;
const double ftol = 1.0e-8;
const size_t n = fdf->n;
const size_t p = fdf->p;
gsl_multifit_nlinear_workspace *work =
gsl_multifit_nlinear_alloc(T, params, n, p);
gsl_vector * f = gsl_multifit_nlinear_residual(work);
gsl_vector * x = gsl_multifit_nlinear_position(work);
int info;
double chisq0, chisq, rcond;
printf("# %s/%s\n",
gsl_multifit_nlinear_name(work),
gsl_multifit_nlinear_trs_name(work));
/* initialize solver */
gsl_multifit_nlinear_init(x0, fdf, work);
/* store initial cost */
gsl_blas_ddot(f, f, &chisq0);
/* iterate until convergence */
gsl_multifit_nlinear_driver(max_iter, xtol, gtol, ftol,
callback, NULL, &info, work);
/* store final cost */
gsl_blas_ddot(f, f, &chisq);
/* store cond(J(x)) */
gsl_multifit_nlinear_rcond(&rcond, work);
/* print summary */
fprintf(stderr, "%-25s %-6zu %-5zu %-5zu %-13.4e %-12.4e %-13.4e (%.2e, %.2e)\n",
gsl_multifit_nlinear_trs_name(work),
gsl_multifit_nlinear_niter(work),
fdf->nevalf,
fdf->nevaldf,
chisq0,
chisq,
1.0 / rcond,
gsl_vector_get(x, 0),
gsl_vector_get(x, 1));
printf("\n\n");
gsl_multifit_nlinear_free(work);
}
int
main (void)
{
const size_t n = 2;
const size_t p = 2;
gsl_vector *f = gsl_vector_alloc(n);
gsl_vector *x = gsl_vector_alloc(p);
gsl_multifit_nlinear_fdf fdf;
gsl_multifit_nlinear_parameters fdf_params =
gsl_multifit_nlinear_default_parameters();
struct model_params params;
params.a1 = -5.1 / (4.0 * M_PI * M_PI);
params.a2 = 5.0 / M_PI;
params.a3 = -6.0;
params.a4 = 10.0;
params.a5 = 1.0 / (8.0 * M_PI);
/* print map of Phi(x1, x2) */
{
double x1, x2, chisq;
for (x1 = -5.0; x1 < 15.0; x1 += 0.1)
{
for (x2 = -5.0; x2 < 15.0; x2 += 0.1)
{
gsl_vector_set(x, 0, x1);
gsl_vector_set(x, 1, x2);
func_f(x, ¶ms, f);
gsl_blas_ddot(f, f, &chisq);
printf("%f %f %f\n", x1, x2, chisq);
}
printf("\n");
}
printf("\n\n");
}
/* define function to be minimized */
fdf.f = func_f;
fdf.df = func_df;
//fdf.fvv = func_fvv;
fdf.n = n;
fdf.p = p;
fdf.params = ¶ms;
/* starting point */
gsl_vector_set(x, 0, 6.0);
gsl_vector_set(x, 1, 14.5);
fprintf(stderr, "%-25s %-6s %-5s %-5s %-13s %-12s %-13s %-15s\n",
"Method", "NITER", "NFEV", "NJEV", "Initial Cost",
"Final cost", "Final cond(J)", "Final x");
fdf_params.trs = gsl_multifit_nlinear_trs_lm;
solve_system(x, &fdf, &fdf_params);
//fdf_params.trs = gsl_multifit_nlinear_trs_lmaccel;
//solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_dogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_ddogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_subspace2D;
solve_system(x, &fdf, &fdf_params);
gsl_vector_free(f);
gsl_vector_free(x);
return 0;
}
Kinda nice to start out with a working example.
Warning: Spoiler!
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_multifit_nlinear.h>
/* parameters to model */
struct model_params
{
double a1;
double a2;
double a3;
double a4;
double a5;
};
/* Branin function */
int
func_f (const gsl_vector * x, void *params, gsl_vector * f)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double x2 = gsl_vector_get(x, 1);
double f1 = x2 + par->a1 * x1 * x1 + par->a2 * x1 + par->a3;
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * cos(x1));
gsl_vector_set(f, 0, f1);
gsl_vector_set(f, 1, f2);
return GSL_SUCCESS;
}
int
func_df (const gsl_vector * x, void *params, gsl_matrix * J)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * cos(x1));
gsl_matrix_set(J, 0, 0, 2.0 * par->a1 * x1 + par->a2);
gsl_matrix_set(J, 0, 1, 1.0);
gsl_matrix_set(J, 1, 0, -0.5 * par->a4 / f2 * (1.0 - par->a5) * sin(x1));
gsl_matrix_set(J, 1, 1, 0.0);
return GSL_SUCCESS;
}
int
func_fvv (const gsl_vector * x, const gsl_vector * v,
void *params, gsl_vector * fvv)
{
struct model_params *par = (struct model_params *) params;
double x1 = gsl_vector_get(x, 0);
double v1 = gsl_vector_get(v, 0);
double c = cos(x1);
double s = sin(x1);
double f2 = sqrt(par->a4) * sqrt(1.0 + (1.0 - par->a5) * c);
double t = 0.5 * par->a4 * (1.0 - par->a5) / f2;
gsl_vector_set(fvv, 0, 2.0 * par->a1 * v1 * v1);
gsl_vector_set(fvv, 1, -t * (c + s*s/f2) * v1 * v1);
return GSL_SUCCESS;
}
void
callback(const size_t iter, void *params,
const gsl_multifit_nlinear_workspace *w)
{
gsl_vector * x = gsl_multifit_nlinear_position(w);
double x1 = gsl_vector_get(x, 0);
double x2 = gsl_vector_get(x, 1);
/* print out current location */
printf("%f %f\n", x1, x2);
}
void
solve_system(gsl_vector *x0, gsl_multifit_nlinear_fdf *fdf,
gsl_multifit_nlinear_parameters *params)
{
const gsl_multifit_nlinear_type *T = gsl_multifit_nlinear_trust;
const size_t max_iter = 200;
const double xtol = 1.0e-8;
const double gtol = 1.0e-8;
const double ftol = 1.0e-8;
const size_t n = fdf->n;
const size_t p = fdf->p;
gsl_multifit_nlinear_workspace *work =
gsl_multifit_nlinear_alloc(T, params, n, p);
gsl_vector * f = gsl_multifit_nlinear_residual(work);
gsl_vector * x = gsl_multifit_nlinear_position(work);
int info;
double chisq0, chisq, rcond;
printf("# %s/%s\n",
gsl_multifit_nlinear_name(work),
gsl_multifit_nlinear_trs_name(work));
/* initialize solver */
gsl_multifit_nlinear_init(x0, fdf, work);
/* store initial cost */
gsl_blas_ddot(f, f, &chisq0);
/* iterate until convergence */
gsl_multifit_nlinear_driver(max_iter, xtol, gtol, ftol,
callback, NULL, &info, work);
/* store final cost */
gsl_blas_ddot(f, f, &chisq);
/* store cond(J(x)) */
gsl_multifit_nlinear_rcond(&rcond, work);
/* print summary */
fprintf(stderr, "%-25s %-6zu %-5zu %-5zu %-13.4e %-12.4e %-13.4e (%.2e, %.2e)\n",
gsl_multifit_nlinear_trs_name(work),
gsl_multifit_nlinear_niter(work),
fdf->nevalf,
fdf->nevaldf,
chisq0,
chisq,
1.0 / rcond,
gsl_vector_get(x, 0),
gsl_vector_get(x, 1));
printf("\n\n");
gsl_multifit_nlinear_free(work);
}
int
main (void)
{
const size_t n = 2;
const size_t p = 2;
gsl_vector *f = gsl_vector_alloc(n);
gsl_vector *x = gsl_vector_alloc(p);
gsl_multifit_nlinear_fdf fdf;
gsl_multifit_nlinear_parameters fdf_params =
gsl_multifit_nlinear_default_parameters();
struct model_params params;
params.a1 = -5.1 / (4.0 * M_PI * M_PI);
params.a2 = 5.0 / M_PI;
params.a3 = -6.0;
params.a4 = 10.0;
params.a5 = 1.0 / (8.0 * M_PI);
/* print map of Phi(x1, x2) */
{
double x1, x2, chisq;
for (x1 = -5.0; x1 < 15.0; x1 += 0.1)
{
for (x2 = -5.0; x2 < 15.0; x2 += 0.1)
{
gsl_vector_set(x, 0, x1);
gsl_vector_set(x, 1, x2);
func_f(x, ¶ms, f);
gsl_blas_ddot(f, f, &chisq);
printf("%f %f %f\n", x1, x2, chisq);
}
printf("\n");
}
printf("\n\n");
}
/* define function to be minimized */
fdf.f = func_f;
fdf.df = func_df;
//fdf.fvv = func_fvv;
fdf.n = n;
fdf.p = p;
fdf.params = ¶ms;
/* starting point */
gsl_vector_set(x, 0, 6.0);
gsl_vector_set(x, 1, 14.5);
fprintf(stderr, "%-25s %-6s %-5s %-5s %-13s %-12s %-13s %-15s\n",
"Method", "NITER", "NFEV", "NJEV", "Initial Cost",
"Final cost", "Final cond(J)", "Final x");
fdf_params.trs = gsl_multifit_nlinear_trs_lm;
solve_system(x, &fdf, &fdf_params);
//fdf_params.trs = gsl_multifit_nlinear_trs_lmaccel;
//solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_dogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_ddogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_subspace2D;
solve_system(x, &fdf, &fdf_params);
gsl_vector_free(f);
gsl_vector_free(x);
return 0;
}
Kinda nice to start out with a working example.
Last edit: 20 Feb 2025 15:23 by Aciera.
The following user(s) said Thank You: akb1212, tommylight, Grotius
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
21 Feb 2025 09:30 - 21 Feb 2025 09:44 #322182
by Aciera
Replied by Aciera on topic scurve trajectory planner
Attachments:
Last edit: 21 Feb 2025 09:44 by Aciera.
The following user(s) said Thank You: Grotius
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
21 Feb 2025 09:40 #322183
by Aciera
Replied by Aciera on topic scurve trajectory planner
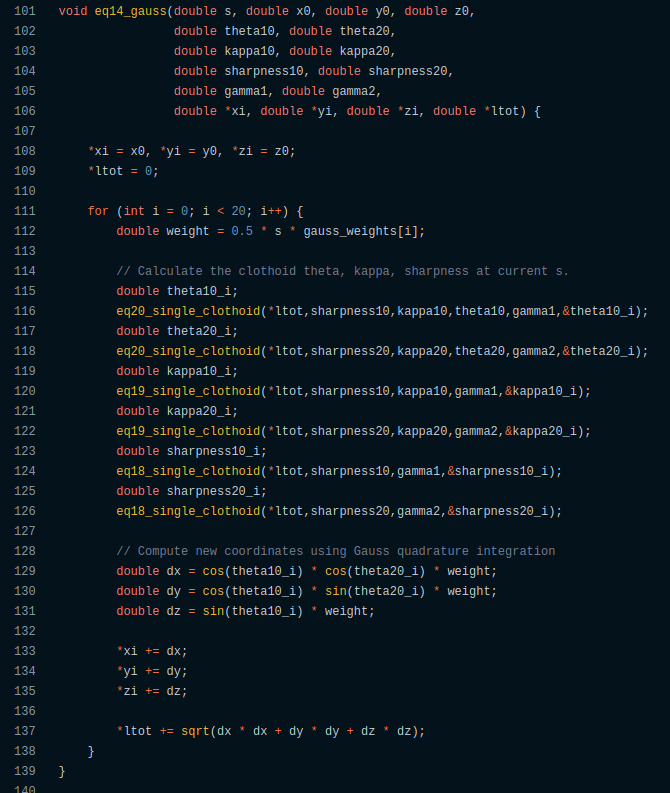
Something like this:
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double sharpness20_i;
eq18_single_clothoid(0,sharpness20,gamma2,&sharpness20_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double kappa20_i;
eq19_single_clothoid(0,sharpness20_i,kappa20_i,gamma2,&kappa20_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
double theta20_i;
eq20_single_clothoid(0,sharpness20_i,kappa20_i,theta20,gamma2,&theta20_i);
The following user(s) said Thank You: akb1212, Grotius
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
21 Feb 2025 09:56 #322185
by Aciera
Replied by Aciera on topic scurve trajectory planner
Here is my failed attempt:
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_multifit_nlinear.h>
/* eq18, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the sharpness for s.
*
*/
void eq18(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *sharpness_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*sharpness_at_s = sharpnessi0 + yi1 * s;
} else if (s > s1 && s <= s2) {
*sharpness_at_s = sharpnessi1 + yi2 * (s - s1);
} else if (s > s2 && s <= s3) {
*sharpness_at_s = sharpnessi2 + yi3 * (s - s2);
} else if (s > s3 && s <= s4) {
*sharpness_at_s = sharpnessi3 + yi4 * (s - s3);
} else {
// Handle the case where s is out of bounds (optional)
*sharpness_at_s = 0.0; // or some other default value
printf("error: eq18. \n");
}
}
void eq18_single_clothoid(const double s,
const double sharpnessi0,
const double yi1,
double *sharpness_at_s) {
*sharpness_at_s = sharpnessi0 + yi1 * s;
}
/* eq19, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the kappa for s.
*
*/
void eq19(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double kappai0, const double kappai1, const double kappai2, const double kappai3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *kappa_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*kappa_at_s = kappai0 + sharpnessi0 * s + 0.5 * yi1 * (s * s);
} else if (s > s1 && s <= s2) {
*kappa_at_s = kappai1 + sharpnessi1 * (s - s1) + 0.5 * yi2 * ((s - s1) * (s - s1));
} else if (s > s2 && s <= s3) {
*kappa_at_s = kappai2 + sharpnessi2 * (s - s2) + 0.5 * yi3 * ((s - s2) * (s - s2));
} else if (s > s3 && s <= s4) {
*kappa_at_s = kappai3 + sharpnessi3 * (s - s3) + 0.5 * yi4 * ((s - s3) * (s - s3));
} else {
// Handle the case where s is out of bounds (optional)
*kappa_at_s = 0.0; // or some other default value
printf("error: eq19. \n");
}
}
void eq19_single_clothoid(const double s,
const double sharpnessi0,
const double kappai0,
const double yi1,
double *kappa_at_s) {
*kappa_at_s = kappai0 + sharpnessi0 * s + 0.5 * yi1 * (s * s);
}
/* eq20, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the theta at s.
*
*/
void eq20(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double kappai0, const double kappai1, const double kappai2, const double kappai3,
const double thetai0, const double thetai1, const double thetai2, const double thetai3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *theta_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*theta_at_s = thetai0 + kappai0 * s + (0.5*sharpnessi0) * (s * s) + (1.0 / 6.0) * yi1 * (s * s * s);
} else if (s > s1 && s <= s2) {
*theta_at_s = thetai1 + kappai1 * (s - s1) + (0.5*sharpnessi1) * ((s - s1) * (s - s1)) + (1.0 / 6.0) * yi2 * ((s - s1) * (s - s1) * (s - s1));
} else if (s > s2 && s <= s3) {
*theta_at_s = thetai2 + kappai2 * (s - s2) + (0.5*sharpnessi2) * ((s - s2) * (s - s2)) + (1.0 / 6.0) * yi3 * ((s - s2) * (s - s2) * (s - s2));
} else if (s > s3 && s <= s4) {
*theta_at_s = thetai3 + kappai3 * (s - s3) + (0.5*sharpnessi3) * ((s - s3) * (s - s3)) + (1.0 / 6.0) * yi4 * ((s - s3) * (s - s3) * (s - s3));
} else {
// Handle the case where s is out of bounds (optional)
*theta_at_s = 0.0; // or some other default value
printf("error: eq20.\n");
}
}
/* Get the theta given s (length) for a single clothoid.
*
*/
void eq20_single_clothoid(const double s,
const double sharpnessi0,
const double kappai0,
const double thetai0,
const double yi1,
double *theta_at_s) {
*theta_at_s = thetai0 + kappai0 * s + (0.5*sharpnessi0) * (s * s) + (1.0 / 6.0) * yi1 * (s * s * s);
}
/* parameters to model */
struct model_params
{
double t10;
double t20;
double k10;
double k20;
double c10;
double c20;
double xs;
double ys;
double zs;
double xe;
double ye;
double ze;
double xi;
double yi;
double zi;
};
/* eq14, page 4
*
* Most efficient and precise solution to compute the clothoid curve lenght.
* Using gauss legendre, up to 20 points. Use a 30 point legendre to get even
* more accuracy.
*
* This calculation is more accurate then the above eq14_drift function.
*
* s = lenght on clothoid to retrieve the xyz point, xi,yi,zi.
* x0 y0 z0 = Clothoid start point.
* ltot = Clothoid length up to s.
*
* gamma1, gamma2, clothoid's rigid body factor. Synonims for y11, y22.
*
*/
float eq14_gauss_x(double s,
double x0, double xe,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_x = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double sharpness20_i;
eq18_single_clothoid(0,sharpness20,gamma2,&sharpness20_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double kappa20_i;
eq19_single_clothoid(0,sharpness20_i,kappa20_i,gamma2,&kappa20_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
double theta20_i;
eq20_single_clothoid(0,sharpness20_i,kappa20_i,theta20,gamma2,&theta20_i);
// Compute new coordinates using Gauss quadrature integration
double dx = cos(theta10_i) * cos(theta20_i) * weight;
sum_x += dx;
}
return x0 + sum_x - xe;
}
float eq14_gauss_y(double s,
double y0, double ye,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_y = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double sharpness20_i;
eq18_single_clothoid(0,sharpness20,gamma2,&sharpness20_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double kappa20_i;
eq19_single_clothoid(0,sharpness20_i,kappa20_i,gamma2,&kappa20_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
double theta20_i;
eq20_single_clothoid(0,sharpness20_i,kappa20_i,theta20,gamma2,&theta20_i);
// Compute new coordinates using Gauss quadrature integration
double dy = cos(theta10_i) * sin(theta20_i) * weight;
sum_y += dy;
}
return y0 + sum_y - ye;
}
float eq14_gauss_z(double s,
double z0, double ze,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_z = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
// Compute new coordinates using Gauss quadrature integration
double dz = sin(theta10_i) * weight;
sum_z += dz;
}
return z0 + sum_z - ze;
}
int
func_f (const gsl_vector * x, void *params, gsl_vector * f)
{
struct model_params *par = (struct model_params *) params;
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
double f1 = eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double f2 = eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double f3 = eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
gsl_vector_set(f, 0, f1);
gsl_vector_set(f, 1, f2);
gsl_vector_set(f, 2, f3);
return GSL_SUCCESS;
}
int
func_df (const gsl_vector * x, void *params, gsl_matrix * J)
{
struct model_params *par = (struct model_params *) params;
double g_delta = 0.001;
double s_delta = 0.001;
double g11 = gsl_vector_get(x, 0);
double dg11 = g11 + g_delta;
double g21 = gsl_vector_get(x, 1);
double dg21 = g21 + g_delta;
double s1 = gsl_vector_get(x, 2);
double ds1 = s1 + s_delta;
// Jacobi 1. row
gsl_matrix_set(J, 0, 0, (eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 0, 1, (eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 0, 2, (eq14_gauss_x(ds1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
// Jacobi 2. row
gsl_matrix_set(J, 1, 0, (eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 1, 1, (eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 1, 2, (eq14_gauss_y(ds1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
// Jacobi 3. row
gsl_matrix_set(J, 2, 0, (eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 2, 1, (eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 2, 2, (eq14_gauss_z(ds1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
return GSL_SUCCESS;
}
void
callback(const size_t iter, void *params,
const gsl_multifit_nlinear_workspace *w)
{
gsl_vector * x = gsl_multifit_nlinear_position(w);
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
/* print out current location */
printf("%f %f %f\n", g11, g21, s1);
}
void
solve_system(gsl_vector *x0, gsl_multifit_nlinear_fdf *fdf,
gsl_multifit_nlinear_parameters *params)
{
const gsl_multifit_nlinear_type *T = gsl_multifit_nlinear_trust;
const size_t max_iter = 200;
const double xtol = 1.0e-8;
const double gtol = 1.0e-8;
const double ftol = 1.0e-8;
const size_t n = fdf->n;
const size_t p = fdf->p;
gsl_multifit_nlinear_workspace *work =
gsl_multifit_nlinear_alloc(T, params, n, p);
gsl_vector * f = gsl_multifit_nlinear_residual(work);
gsl_vector * x = gsl_multifit_nlinear_position(work);
int info;
double chisq0, chisq, rcond;
printf("# %s/%s\n",
gsl_multifit_nlinear_name(work),
gsl_multifit_nlinear_trs_name(work));
/* initialize solver */
gsl_multifit_nlinear_init(x0, fdf, work);
/* store initial cost */
gsl_blas_ddot(f, f, &chisq0);
/* iterate until convergence */
gsl_multifit_nlinear_driver(max_iter, xtol, gtol, ftol,
callback, NULL, &info, work);
/* store final cost */
gsl_blas_ddot(f, f, &chisq);
/* store cond(J(x)) */
gsl_multifit_nlinear_rcond(&rcond, work);
printf("\n");
struct model_params *par = (struct model_params *) params;
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
double x_res = eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double y_res = eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double z_res = eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
printf("Position Error: (%f %f %f)\n", x_res, y_res, z_res);
/* print summary */
fprintf(stderr, "%-25s %-6zu %-5zu %-5zu %-13.4e %-12.4e %-13.4e (%.2e, %.2e, %.2e)\n",
gsl_multifit_nlinear_trs_name(work),
gsl_multifit_nlinear_niter(work),
fdf->nevalf,
fdf->nevaldf,
chisq0,
chisq,
1.0 / rcond,
gsl_vector_get(x, 0),
gsl_vector_get(x, 1),
gsl_vector_get(x, 2));
printf("\n\n");
gsl_multifit_nlinear_free(work);
}
int
main (void)
{
const size_t n = 3;
const size_t p = 3;
gsl_vector *f = gsl_vector_alloc(n);
gsl_vector *x = gsl_vector_alloc(p);
gsl_multifit_nlinear_fdf fdf;
gsl_multifit_nlinear_parameters fdf_params =
gsl_multifit_nlinear_default_parameters();
struct model_params params;
params.t10 = 45.0 * (M_PI / 180.0);
params.t20 = 0.0 * (M_PI / 180.0);
params.k10 = 0.0;
params.k20 = 0.0;
params.c10 = 0.0;
params.c20 = 0.0;
params.xs = 0.0;
params.ys = 0.0;
params.zs = 0.0;
params.xe = 11.11;
params.ye = 22.22;
params.ze = 33.33;
params.xi;
params.yi;
params.zi;
/*
// print map of Phi(x1, x2)
{
double g11, g21, s1, chisq;
for (g11 = -5.0; g11 < 15.0; g11 += 0.1)
{
for (g21 = -5.0; g21 < 15.0; g21 += 0.1)
{
for (s1 = -5.0; s1 < 15.0; s1 += 0.1)
{
gsl_vector_set(x, 0, g11);
gsl_vector_set(x, 1, g21);
gsl_vector_set(x, 2, s1);
func_f(x, ¶ms, f);
gsl_blas_ddot(f, f, &chisq);
printf("%f %f %f %f\n", g11, g21, s1, chisq);
}
printf("\n");
}
printf("\n");
}
printf("\n\n");
}
/* define function to be minimized */
fdf.f = func_f;
fdf.df = func_df;
fdf.n = n;
fdf.p = p;
fdf.params = ¶ms;
/* starting point */
gsl_vector_set(x, 0, 0.01);
gsl_vector_set(x, 1, 0.01);
gsl_vector_set(x, 2, 0.01);
fprintf(stderr, "%-25s %-6s %-5s %-5s %-13s %-12s %-13s %-15s\n",
"Method", "NITER", "NFEV", "NJEV", "Initial Cost",
"Final cost", "Final cond(J)", "Final x");
fdf_params.trs = gsl_multifit_nlinear_trs_lm;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_dogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_ddogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_subspace2D;
solve_system(x, &fdf, &fdf_params);
gsl_vector_free(f);
gsl_vector_free(x);
return 0;
}
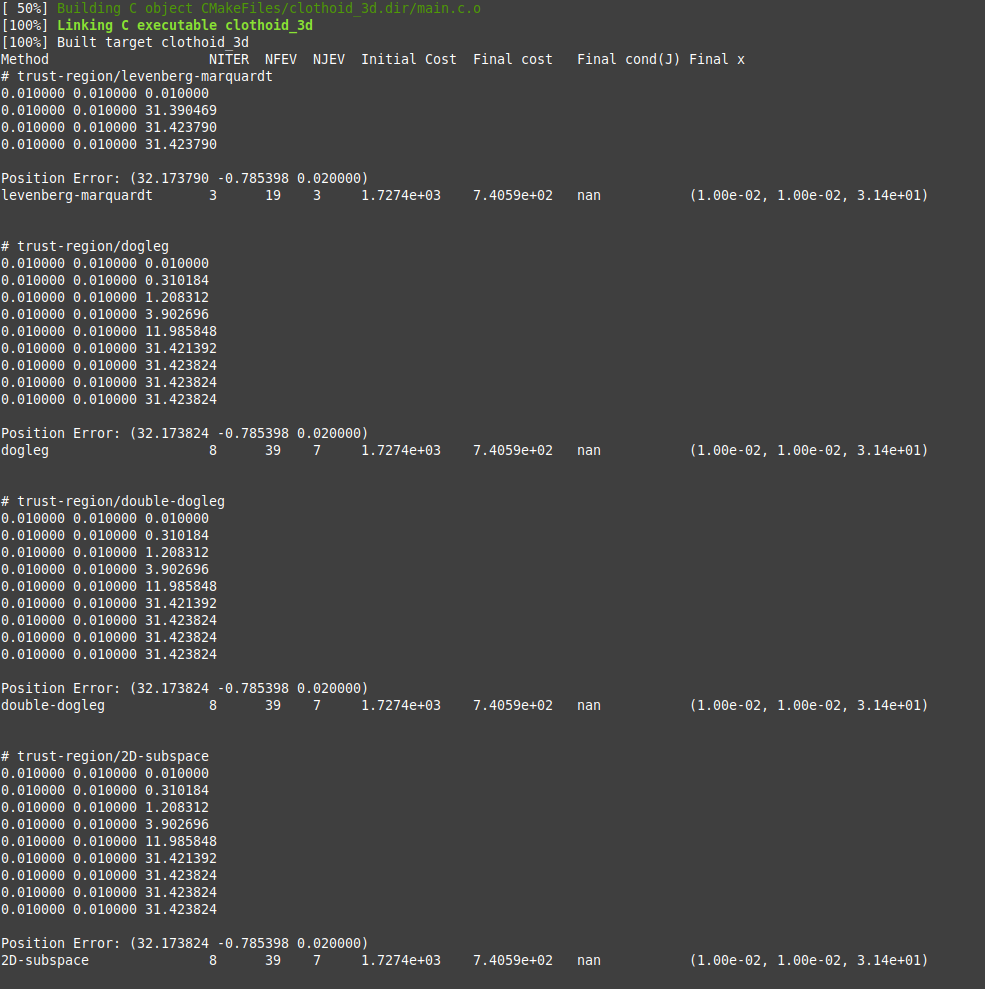
The idea was to calculate the elements of the Jacobian numerically but it fails miserably:
Warning: Spoiler!
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_multifit_nlinear.h>
/* eq18, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the sharpness for s.
*
*/
void eq18(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *sharpness_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*sharpness_at_s = sharpnessi0 + yi1 * s;
} else if (s > s1 && s <= s2) {
*sharpness_at_s = sharpnessi1 + yi2 * (s - s1);
} else if (s > s2 && s <= s3) {
*sharpness_at_s = sharpnessi2 + yi3 * (s - s2);
} else if (s > s3 && s <= s4) {
*sharpness_at_s = sharpnessi3 + yi4 * (s - s3);
} else {
// Handle the case where s is out of bounds (optional)
*sharpness_at_s = 0.0; // or some other default value
printf("error: eq18. \n");
}
}
void eq18_single_clothoid(const double s,
const double sharpnessi0,
const double yi1,
double *sharpness_at_s) {
*sharpness_at_s = sharpnessi0 + yi1 * s;
}
/* eq19, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the kappa for s.
*
*/
void eq19(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double kappai0, const double kappai1, const double kappai2, const double kappai3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *kappa_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*kappa_at_s = kappai0 + sharpnessi0 * s + 0.5 * yi1 * (s * s);
} else if (s > s1 && s <= s2) {
*kappa_at_s = kappai1 + sharpnessi1 * (s - s1) + 0.5 * yi2 * ((s - s1) * (s - s1));
} else if (s > s2 && s <= s3) {
*kappa_at_s = kappai2 + sharpnessi2 * (s - s2) + 0.5 * yi3 * ((s - s2) * (s - s2));
} else if (s > s3 && s <= s4) {
*kappa_at_s = kappai3 + sharpnessi3 * (s - s3) + 0.5 * yi4 * ((s - s3) * (s - s3));
} else {
// Handle the case where s is out of bounds (optional)
*kappa_at_s = 0.0; // or some other default value
printf("error: eq19. \n");
}
}
void eq19_single_clothoid(const double s,
const double sharpnessi0,
const double kappai0,
const double yi1,
double *kappa_at_s) {
*kappa_at_s = kappai0 + sharpnessi0 * s + 0.5 * yi1 * (s * s);
}
/* eq20, page 4.
*
* stot = total clothoid length
* s = global length at clothoid to retrieve sharpness c.
*
* Retrieve the theta at s.
*
*/
void eq20(const double s, const double stot,
const double sharpnessi0, const double sharpnessi1, const double sharpnessi2, const double sharpnessi3,
const double kappai0, const double kappai1, const double kappai2, const double kappai3,
const double thetai0, const double thetai1, const double thetai2, const double thetai3,
const double yi1, const double yi2, const double yi3, const double yi4,
double *theta_at_s) {
double s1 = stot / 4.0;
double s2 = s1 + s1;
double s3 = s1 + s1 + s1;
double s4 = stot;
if (s <= s1) {
*theta_at_s = thetai0 + kappai0 * s + (0.5*sharpnessi0) * (s * s) + (1.0 / 6.0) * yi1 * (s * s * s);
} else if (s > s1 && s <= s2) {
*theta_at_s = thetai1 + kappai1 * (s - s1) + (0.5*sharpnessi1) * ((s - s1) * (s - s1)) + (1.0 / 6.0) * yi2 * ((s - s1) * (s - s1) * (s - s1));
} else if (s > s2 && s <= s3) {
*theta_at_s = thetai2 + kappai2 * (s - s2) + (0.5*sharpnessi2) * ((s - s2) * (s - s2)) + (1.0 / 6.0) * yi3 * ((s - s2) * (s - s2) * (s - s2));
} else if (s > s3 && s <= s4) {
*theta_at_s = thetai3 + kappai3 * (s - s3) + (0.5*sharpnessi3) * ((s - s3) * (s - s3)) + (1.0 / 6.0) * yi4 * ((s - s3) * (s - s3) * (s - s3));
} else {
// Handle the case where s is out of bounds (optional)
*theta_at_s = 0.0; // or some other default value
printf("error: eq20.\n");
}
}
/* Get the theta given s (length) for a single clothoid.
*
*/
void eq20_single_clothoid(const double s,
const double sharpnessi0,
const double kappai0,
const double thetai0,
const double yi1,
double *theta_at_s) {
*theta_at_s = thetai0 + kappai0 * s + (0.5*sharpnessi0) * (s * s) + (1.0 / 6.0) * yi1 * (s * s * s);
}
/* parameters to model */
struct model_params
{
double t10;
double t20;
double k10;
double k20;
double c10;
double c20;
double xs;
double ys;
double zs;
double xe;
double ye;
double ze;
double xi;
double yi;
double zi;
};
/* eq14, page 4
*
* Most efficient and precise solution to compute the clothoid curve lenght.
* Using gauss legendre, up to 20 points. Use a 30 point legendre to get even
* more accuracy.
*
* This calculation is more accurate then the above eq14_drift function.
*
* s = lenght on clothoid to retrieve the xyz point, xi,yi,zi.
* x0 y0 z0 = Clothoid start point.
* ltot = Clothoid length up to s.
*
* gamma1, gamma2, clothoid's rigid body factor. Synonims for y11, y22.
*
*/
float eq14_gauss_x(double s,
double x0, double xe,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_x = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double sharpness20_i;
eq18_single_clothoid(0,sharpness20,gamma2,&sharpness20_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double kappa20_i;
eq19_single_clothoid(0,sharpness20_i,kappa20_i,gamma2,&kappa20_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
double theta20_i;
eq20_single_clothoid(0,sharpness20_i,kappa20_i,theta20,gamma2,&theta20_i);
// Compute new coordinates using Gauss quadrature integration
double dx = cos(theta10_i) * cos(theta20_i) * weight;
sum_x += dx;
}
return x0 + sum_x - xe;
}
float eq14_gauss_y(double s,
double y0, double ye,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_y = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double sharpness20_i;
eq18_single_clothoid(0,sharpness20,gamma2,&sharpness20_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double kappa20_i;
eq19_single_clothoid(0,sharpness20_i,kappa20_i,gamma2,&kappa20_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
double theta20_i;
eq20_single_clothoid(0,sharpness20_i,kappa20_i,theta20,gamma2,&theta20_i);
// Compute new coordinates using Gauss quadrature integration
double dy = cos(theta10_i) * sin(theta20_i) * weight;
sum_y += dy;
}
return y0 + sum_y - ye;
}
float eq14_gauss_z(double s,
double z0, double ze,
double theta10, double theta20,
double kappa10, double kappa20,
double sharpness10, double sharpness20,
double gamma1, double gamma2) {
// Gauss-Legendre 20-point weights & nodes
const double gauss_weights[20] = {
0.1527533871, 0.1491729865, 0.1420961093, 0.1316886384, 0.1181945319,
0.1019301198, 0.0832767416, 0.0626720483, 0.0406014298, 0.0176140071,
0.0176140071, 0.0406014298, 0.0626720483, 0.0832767416, 0.1019301198,
0.1181945319, 0.1316886384, 0.1420961093, 0.1491729865, 0.1527533871
};
const double gauss_nodes[20] = {
-0.9931285992, -0.9639719273, -0.9122344283, -0.8391169718, -0.7463319065,
-0.6360536807, -0.5108670019, -0.3737060887, -0.2277858511, -0.0765265211,
0.0765265211, 0.2277858511, 0.3737060887, 0.5108670019, 0.6360536807,
0.7463319065, 0.8391169718, 0.9122344283, 0.9639719273, 0.9931285992
};
double sum_z = 0.0;
for (int i = 0; i < 20; i++) {
double weight = 0.5 * s * gauss_weights;
// Calculate the clothoid theta, kappa, sharpness at current s.
// Calculate the clothoid theta, kappa, sharpness at current s.
double sharpness10_i;
eq18_single_clothoid(0,sharpness10,gamma1,&sharpness10_i);
double kappa10_i;
eq19_single_clothoid(0,sharpness10_i,kappa10_i,gamma1,&kappa10_i);
double theta10_i;
eq20_single_clothoid(0,sharpness10_i,kappa10_i,theta10,gamma1,&theta10_i);
// Compute new coordinates using Gauss quadrature integration
double dz = sin(theta10_i) * weight;
sum_z += dz;
}
return z0 + sum_z - ze;
}
int
func_f (const gsl_vector * x, void *params, gsl_vector * f)
{
struct model_params *par = (struct model_params *) params;
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
double f1 = eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double f2 = eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double f3 = eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
gsl_vector_set(f, 0, f1);
gsl_vector_set(f, 1, f2);
gsl_vector_set(f, 2, f3);
return GSL_SUCCESS;
}
int
func_df (const gsl_vector * x, void *params, gsl_matrix * J)
{
struct model_params *par = (struct model_params *) params;
double g_delta = 0.001;
double s_delta = 0.001;
double g11 = gsl_vector_get(x, 0);
double dg11 = g11 + g_delta;
double g21 = gsl_vector_get(x, 1);
double dg21 = g21 + g_delta;
double s1 = gsl_vector_get(x, 2);
double ds1 = s1 + s_delta;
// Jacobi 1. row
gsl_matrix_set(J, 0, 0, (eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 0, 1, (eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 0, 2, (eq14_gauss_x(ds1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
// Jacobi 2. row
gsl_matrix_set(J, 1, 0, (eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 1, 1, (eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 1, 2, (eq14_gauss_y(ds1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
// Jacobi 3. row
gsl_matrix_set(J, 2, 0, (eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
dg11, g21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 2, 1, (eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, dg21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / g_delta
);
gsl_matrix_set(J, 2, 2, (eq14_gauss_z(ds1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21) -
eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21)) / s_delta
);
return GSL_SUCCESS;
}
void
callback(const size_t iter, void *params,
const gsl_multifit_nlinear_workspace *w)
{
gsl_vector * x = gsl_multifit_nlinear_position(w);
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
/* print out current location */
printf("%f %f %f\n", g11, g21, s1);
}
void
solve_system(gsl_vector *x0, gsl_multifit_nlinear_fdf *fdf,
gsl_multifit_nlinear_parameters *params)
{
const gsl_multifit_nlinear_type *T = gsl_multifit_nlinear_trust;
const size_t max_iter = 200;
const double xtol = 1.0e-8;
const double gtol = 1.0e-8;
const double ftol = 1.0e-8;
const size_t n = fdf->n;
const size_t p = fdf->p;
gsl_multifit_nlinear_workspace *work =
gsl_multifit_nlinear_alloc(T, params, n, p);
gsl_vector * f = gsl_multifit_nlinear_residual(work);
gsl_vector * x = gsl_multifit_nlinear_position(work);
int info;
double chisq0, chisq, rcond;
printf("# %s/%s\n",
gsl_multifit_nlinear_name(work),
gsl_multifit_nlinear_trs_name(work));
/* initialize solver */
gsl_multifit_nlinear_init(x0, fdf, work);
/* store initial cost */
gsl_blas_ddot(f, f, &chisq0);
/* iterate until convergence */
gsl_multifit_nlinear_driver(max_iter, xtol, gtol, ftol,
callback, NULL, &info, work);
/* store final cost */
gsl_blas_ddot(f, f, &chisq);
/* store cond(J(x)) */
gsl_multifit_nlinear_rcond(&rcond, work);
printf("\n");
struct model_params *par = (struct model_params *) params;
double g11 = gsl_vector_get(x, 0);
double g21 = gsl_vector_get(x, 1);
double s1 = gsl_vector_get(x, 2);
double x_res = eq14_gauss_x(s1,
par->xs, par->xe,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double y_res = eq14_gauss_y(s1,
par->ys, par->ye,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
double z_res = eq14_gauss_z(s1,
par->zs, par->ze,
par->t10, par->t20,
par->k10, par->k20,
par->c10, par->c20,
g11, g21);
printf("Position Error: (%f %f %f)\n", x_res, y_res, z_res);
/* print summary */
fprintf(stderr, "%-25s %-6zu %-5zu %-5zu %-13.4e %-12.4e %-13.4e (%.2e, %.2e, %.2e)\n",
gsl_multifit_nlinear_trs_name(work),
gsl_multifit_nlinear_niter(work),
fdf->nevalf,
fdf->nevaldf,
chisq0,
chisq,
1.0 / rcond,
gsl_vector_get(x, 0),
gsl_vector_get(x, 1),
gsl_vector_get(x, 2));
printf("\n\n");
gsl_multifit_nlinear_free(work);
}
int
main (void)
{
const size_t n = 3;
const size_t p = 3;
gsl_vector *f = gsl_vector_alloc(n);
gsl_vector *x = gsl_vector_alloc(p);
gsl_multifit_nlinear_fdf fdf;
gsl_multifit_nlinear_parameters fdf_params =
gsl_multifit_nlinear_default_parameters();
struct model_params params;
params.t10 = 45.0 * (M_PI / 180.0);
params.t20 = 0.0 * (M_PI / 180.0);
params.k10 = 0.0;
params.k20 = 0.0;
params.c10 = 0.0;
params.c20 = 0.0;
params.xs = 0.0;
params.ys = 0.0;
params.zs = 0.0;
params.xe = 11.11;
params.ye = 22.22;
params.ze = 33.33;
params.xi;
params.yi;
params.zi;
/*
// print map of Phi(x1, x2)
{
double g11, g21, s1, chisq;
for (g11 = -5.0; g11 < 15.0; g11 += 0.1)
{
for (g21 = -5.0; g21 < 15.0; g21 += 0.1)
{
for (s1 = -5.0; s1 < 15.0; s1 += 0.1)
{
gsl_vector_set(x, 0, g11);
gsl_vector_set(x, 1, g21);
gsl_vector_set(x, 2, s1);
func_f(x, ¶ms, f);
gsl_blas_ddot(f, f, &chisq);
printf("%f %f %f %f\n", g11, g21, s1, chisq);
}
printf("\n");
}
printf("\n");
}
printf("\n\n");
}
/* define function to be minimized */
fdf.f = func_f;
fdf.df = func_df;
fdf.n = n;
fdf.p = p;
fdf.params = ¶ms;
/* starting point */
gsl_vector_set(x, 0, 0.01);
gsl_vector_set(x, 1, 0.01);
gsl_vector_set(x, 2, 0.01);
fprintf(stderr, "%-25s %-6s %-5s %-5s %-13s %-12s %-13s %-15s\n",
"Method", "NITER", "NFEV", "NJEV", "Initial Cost",
"Final cost", "Final cond(J)", "Final x");
fdf_params.trs = gsl_multifit_nlinear_trs_lm;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_dogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_ddogleg;
solve_system(x, &fdf, &fdf_params);
fdf_params.trs = gsl_multifit_nlinear_trs_subspace2D;
solve_system(x, &fdf, &fdf_params);
gsl_vector_free(f);
gsl_vector_free(x);
return 0;
}
The idea was to calculate the elements of the Jacobian numerically but it fails miserably:
Attachments:
The following user(s) said Thank You: akb1212, Grotius
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-
Less
More
- Posts: 2419
- Thank you received: 2348
21 Feb 2025 09:58 #322186
by Grotius
Replied by Grotius on topic scurve trajectory planner
@Arciera,
Indeed. Good spot !!!
I was thinking about the 3d fitting between gcode segments.
Do we really need the transformation, and then do the fitting in a null plane?
This was needed for a 2d clothoid, when used in a 3d plane. But for this i think
we don't needed, unless there is something i forgot.
I thought maybe we can just fit the clothoids in 3d space.
Indeed. Good spot !!!
I was thinking about the 3d fitting between gcode segments.
Do we really need the transformation, and then do the fitting in a null plane?
This was needed for a 2d clothoid, when used in a 3d plane. But for this i think
we don't needed, unless there is something i forgot.
I thought maybe we can just fit the clothoids in 3d space.
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
21 Feb 2025 10:06 #322188
by Aciera
Replied by Aciera on topic scurve trajectory planner
As i understand it there should be no need for another transformation besides the one described in the paper.
The following user(s) said Thank You: Grotius
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-
Less
More
- Posts: 2419
- Thank you received: 2348
21 Feb 2025 10:10 - 21 Feb 2025 13:04 #322189
by Grotius
Replied by Grotius on topic scurve trajectory planner
@Arciera,
That's what i think we don't need. If the dogleg solver is able to find the endpoint in 3d space. Why do the tranformations
as used in the abstract?
We have already a case where the helix tail or start from a G2, G3 is used as end vector.
I see you have splitted up the gaus interpolation into x, y, z.
Edit:
Did a mayor update on the infrastructure.
- Use struct for clothoid data.
- Use seperate plot function.
- Use enum to choose a solver from the list.
- Use a central residual function used by all solvers. Where the objective function can cast types.
That's what i think we don't need. If the dogleg solver is able to find the endpoint in 3d space. Why do the tranformations
as used in the abstract?
We have already a case where the helix tail or start from a G2, G3 is used as end vector.
I see you have splitted up the gaus interpolation into x, y, z.
Edit:
Did a mayor update on the infrastructure.
- Use struct for clothoid data.
- Use seperate plot function.
- Use enum to choose a solver from the list.
- Use a central residual function used by all solvers. Where the objective function can cast types.
Last edit: 21 Feb 2025 13:04 by Grotius.
The following user(s) said Thank You: akb1212, Aciera
Please Log in or Create an account to join the conversation.
- Aciera
-

- Offline
- Administrator
-

Less
More
- Posts: 4661
- Thank you received: 2078
21 Feb 2025 13:16 - 21 Feb 2025 13:43 #322202
by Aciera
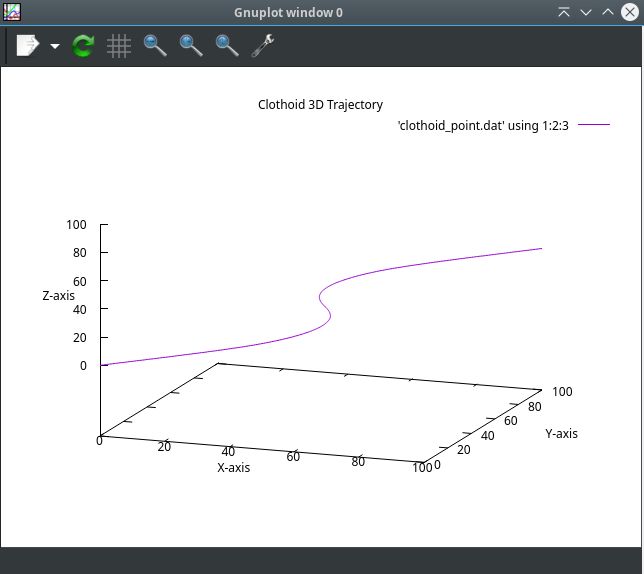
Well that's just a rough hack really that would need some streamlining but as long as nothing converges there is no point in polishing.
[edit]
And it looks like I have done it wrong having set ltot to 0
Replied by Aciera on topic scurve trajectory planner
Can't give you a definite answer to that but as long as we can't do it as described in the paper is seems a bit premature to want to modify the described method.Why do the tranformations as used in the abstract?
I see you have splitted up the gaus interpolation into x, y, z.
Well that's just a rough hack really that would need some streamlining but as long as nothing converges there is no point in polishing.
[edit]
And it looks like I have done it wrong having set ltot to 0
Last edit: 21 Feb 2025 13:43 by Aciera.
The following user(s) said Thank You: akb1212, Grotius
Please Log in or Create an account to join the conversation.
- FabianB
-

- Offline
- New Member
-

Less
More
- Posts: 14
- Thank you received: 19
21 Feb 2025 14:05 #322203
by FabianB
Replied by FabianB on topic scurve trajectory planner
Hi guys,
looks like you are making good progress. Short question regarding the single_clothoid_fit() are you only fitting the start and endpoint or are you also trying to match the curvature etc.?
looks like you are making good progress. Short question regarding the single_clothoid_fit() are you only fitting the start and endpoint or are you also trying to match the curvature etc.?
The following user(s) said Thank You: Grotius
Please Log in or Create an account to join the conversation.
- Grotius
-
 Topic Author
Topic Author
- Offline
- Platinum Member
-
Less
More
- Posts: 2419
- Thank you received: 2348
21 Feb 2025 15:03 #322207
by Grotius
Replied by Grotius on topic scurve trajectory planner
@Arciera,
The only motivation in the abstract is to align the normal n with the positive z axis direction.
The equatations for the math are already there.
- Added clothoid interpolation
- Added dynamic plot size
@Fabian,
looks like you are making good progress.
Yes. To be honest. I did not know we could do this at all. My math level is not that good.
The progress is fenominal. We now have at least a working solution.
We can now refine, polish code and add different solvers to the codebase. Arciera is hard
working to try out new non-linear solvers, wich are kind off trickie to set up.
The result is a G3 solution between previous and next gcode segment.
Indeed, it matches curvature.
Later on we can test more graphical in opencascade. Wich has also a great codebase
to do forward & inverse transformations.
And maybe, maybe i will code a bi-clothoid in the future. As a 4-clothoid can cause overfitting,
wich is inherent to higher degree curves.
The only motivation in the abstract is to align the normal n with the positive z axis direction.
The equatations for the math are already there.
- Added clothoid interpolation
- Added dynamic plot size
@Fabian,
looks like you are making good progress.
Yes. To be honest. I did not know we could do this at all. My math level is not that good.
The progress is fenominal. We now have at least a working solution.
We can now refine, polish code and add different solvers to the codebase. Arciera is hard
working to try out new non-linear solvers, wich are kind off trickie to set up.
The result is a G3 solution between previous and next gcode segment.
Indeed, it matches curvature.
Later on we can test more graphical in opencascade. Wich has also a great codebase
to do forward & inverse transformations.
And maybe, maybe i will code a bi-clothoid in the future. As a 4-clothoid can cause overfitting,
wich is inherent to higher degree curves.
Attachments:
The following user(s) said Thank You: akb1212
Please Log in or Create an account to join the conversation.
Time to create page: 0.175 seconds